Welcome to Narcissus's Blog!
这里是Narcissus的技术圈-
RNN原理、公式推导及python实现
RNN原理及pytorch实现
图像理解
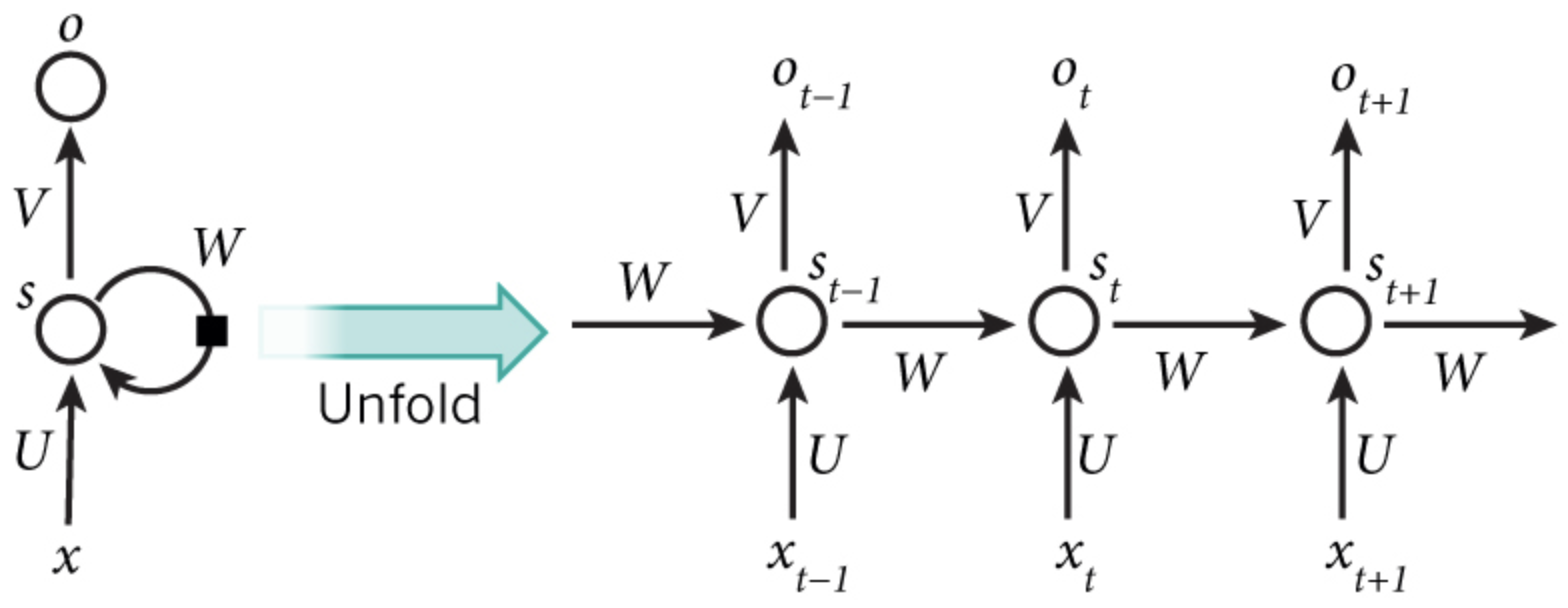
注意细节
- RNN只有这四个参数:$U,W$,对于RNN和特定任务相结合,使用隐藏状态的输出,得到预测结果,也就是分类器部分,才有分类器的参数$V$,并不是RNN的参数。
-
横向展开的每个timestep共享权重。
-
pytorch中的激活函数:tanh 或者 relu,因为pytorch直接使用的cudnn接口,cudnn中只支持这两种。
-
pytorch中,RNN的默认输入形状是(seq_len, batch_size, input_size),batch_size位于第二维度,因为cuDNN中RNN的API就是batch_size在第二维度!把batch_first设置为True,可以将batch_size和序列长度seq_len对换位置。batch first意味着模型的输入(一个Tensor)在内存中存储时,先存储第一个sequence,再存储第二个… 而如果是seq_len first,模型的输入在内存中,先存储所有序列的第一个单元,然后是第二个单元.

公式理解
正向传播公式
RNN迭代式 分类器 损失:把整个timestep的数据当成一个训练数据。
反向求导(BPTT:back propagation through time)
BPTT是关于标准RNN的名称。对每个参数的求导,都要各个timestep加起来。即:

以$\frac{\partial{E_1}}{\partial{W}}$为例:


1)$V$的反向求导比较简单,,与等无时间序列无关
-
Word Embedding models的深入理解
显示不正常可看pdf版本
Word Embedding 深入理解
Well-known models for learning word embeddings based on language modelling. 这些无监督方法学得的词向量已经在很多NLP任务中代替了传统的“分布式特征”(distributional feature,since the underlying semantic theory is called distributional semantics),比如Brown clusters以及LSA 特征。如今盛行的Word Embedding都是指的“dense representations of words in a low-dimensional vector space”,还可以表示为word vectors , distributed representations, semantic vector space or simply word space。Word Embedding表示的向量能表示语义相似性,可以用来表示自身的语义特征,计算不同词之间的语义相似性,也可以作为一种表示,应用到其他NLP任务中去,like text classification, document clustering, part of speech tagging, named entity recognition, sentiment analysis, and so on.
Distributional Semantics History
Idea: 相对于形式化的语言学,语言上下文信息能形成一个合理的关于语言项(如word)的表示。
19世纪八九十年代就有这种semantic representation的应用。Methods for using automatically generated contextual features were developed more or less simultaneously around 1990 in several different research areas. LSA/LSI就是最有影响力的模型,也是现今topic models的先驱;与此同时也有利用这些contextual representation的人工神经网络模型,如SOM,SRN,他们是如今神经语言模型的先驱。
后来的模型几乎都是对原有模型的一些细微改良,比如topic models里面的PLSA,LDA都是对LSA的改良;neural language moddel基于SRN、CNN、Autoencoders等。Distrubutional semantic models都是基于HAL等。主要区别是他们使用的是不同类型的contextual information,而不同的上下文信息表达了不同的语义相似性。
The main difference between these various models is the type of contextual information they use. LSA and topic models use documents as contexts, which is a legacy from their roots in information retrieval. Neural language models and distributional semantic models instead use words as contexts, which is arguably more natural from a linguistic and cognitive perspective. These different contextual representations capture different types of semantic similarity; the document-based models capture semantic relatedness (e.g. “boat” – “water”) while the word-based models capture semantic similarity (e.g. “boat” – “ship”). This very basic difference is too often misunderstood.
这里对于普遍的错误认识还有两个点需要说明:
- 没必要为了得到好的word embedding而使用深度神经网络模型,因为目前的CBOW和Skip-gram模型都是和SRN相似的浅层神经网络模型,却已经取得了比较成功的效果。
- There is no qualitative difference between (current) predictive* neural network models and count-based distributional semantics models. Rather, they are different computational means to arrive at the same type of semantic model。
那么现在最新的一些语义模型怎么样呢?
What about the current state of the art? The boring answer is that it depends on what task you want to solve, and how much effort you want to spend on optimizing the model.(现在的模型取决于你要解决什么样的任务以及你对模型的优化做了多大努力) The somewhat more enjoyable answer is that you will probably do fine whichever current method you choose, since they are more or less equivalent(无论你选择哪个模型,你都能取得差不多较好的效果,因为他们多多少少都是等同的). A good bet is to use a factorized model – either using explicit factorization of a distributional semantic model (available in e.g. the PyDSM python library or the GloVeimplementation), or using a neural network model like those implemented in word2vec – since they produce state of the art results (Österlund et al., 2015) and are robust across a wide range of semantic tasks (Schnabel et al., 2015).
Word Embedding History
2003, Bengio et al.提出术语“word embedding”,并训练神经网络参数;
2008年,Collobert and Weston 提出预训练word embedding的应用;
2013年,Mikolov et al. 提出了最受欢迎的 word2vec 允许无缝训练以及使用预训练word embedding;
2014年,Pennington et al. 放出GloVe.
词向量是少数无监督学习的成功应用。 they don’t require expensive annotation, can be derived from large unannotated corpora that are readily available. Pre-trained embeddings can then be used in downstream tasks that use small amounts of labeled data.
Word embedding models
Embedding Layer
在神经网络中,语料通过词典表示后作为输入,然后通过网络第一层将输入embed成低维向量,这个第一维就是Embedding Layer。但这些方法和Word2vec是有所区别的,前者将word embedding当作一个副产品输出,而后者则明确的将Word embedding的生成作为目标,两者的区别就是:
1)计算复杂度的不一样,计算复杂度是一个非常关键的问题,通过深度神经网络来生成word embedding是很昂贵的,这也就是为什么2013年才火起来的原因。
2)训练目标不一样。word2vec和glove是产生的通用word embedding relationship,对那些不依赖这种相似性的任务来说,并不能产生太大帮助的,比如boat和ship比较具有相关性,而有些任务中可能需要boat和water具有相关性;但是regular neural network不一样,他们产生的是task-specific的embeddings。对于依赖于semantically coherent representations的任务,如语言模型,会和word embedding models产生相似的word embedding。
Word embedding models are often evaluated using perplexity, a cross-entropy based measure borrowed from language modelling.
notational standards
- T training words $w_1, w_2, w_3, \cdots, w_T$
- vocabulary V
- context of n words
- input embedding $v_w$
- input embedding $v’_w$
- model outputs some score $f_\theta(x)$
- Objective function $J_\theta$
Language Modelling
Task:基于n-gram语言模型: 给定n-1个前面的词,计算下一个词的概率:$p(w_t : : w_{t-1} , \cdots w_{t-n+1})$ 基于链式法则和Markov假设,整个sentence或者document的概率就是: 如何计算每个词的概率呢?可以根据n-gram出现的频率来计算: 而在神经网络模型中,就是通过下面softmax计算得到: $h^\top v’_{w_t}$ computes the (unnormalized) log-probability of word $w_t$, h是网络倒数第二层的输出,we normalize by the sum of the log-probabilities of all words in V,which is computation expensive.
目标函数:
Classic neural language model
Their model maximizes what we’ve described above as the prototypical neural language model objective (we omit the regularization term for simplicity):

Figure 2: Classic neural language model (Bengio et al., 2003) The general building blocks of their model, however, are still found in all current neural language and word embedding models. These are:(这些层现在的模型中还被使用)
- Embedding Layer: a layer that generates word embeddings by multiplying an index vector with a word embedding matrix;
- Intermediate Layer(s): one or more layers that produce an intermediate representation of the input, e.g. a fully-connected layer that applies a non-linearity to the concatenation of word embeddings of nn previous words;//这一项可以用LSTM代替
- Softmax Layer: the final layer that produces a probability distribution over words in V.//这一项的计算量非常大,one of the key challenges both in neural language models as well as in word embedding models.
C&W model
Word embeddings trained on a sufficiently large dataset carry syntactic and semantic meaning and improve performance on downstream tasks.为了解决计算量的问题,他们使用了新的loss,ranking objective,而不再使用softmax+CE,这个loss能为正确的单词序列产生比错误序列更高的分数,他们使用了一个pairwise ranking criterion: 这里是一个hinge loss,其中$x^{w}$是采样的负样本,x为正样本。正样本分数要比负样本的分数至少高1.

Figure 3: The C&W model without ranking objective (Collobert et al., 2011)
-
从EncoderDecoder到Transformer
[TOC]
可能显示有点问题,可查看pdf:https://github.com/Narcissuscyn/Algorithm/blob/master/from_encoder_decoder_to_transformer.pdf
Encoder-Decoder
在Quara上有一个问题:https://www.quora.com/What-is-an-Encoder-Decoder-in-Deep-Learning,其中Rohan Saxena的回答我觉得挺好理解的,从横向和纵向两个方向来解释这个问题。
横向分析
首先说了特征表示在机器学习里面的重要性,从早期的手工特征(如HOG)到现在使用神经网络进行特征学习(The first few layers of a neural network extract features from the data, or in other words map raw inputs to efficient feature representations. The next few layers (typically fully connected layers) mix and match and combine these features to produce an output.),都是为了得到好的特征表达。
而一些网络结构被设计用来提取有效的特征表达:
They use an encoder network to map raw inputs to feature representations, and a decoder network to take this feature representation as input, process it to make its decision, and produce an output. This is called an encoder-decoder network.
encoder和decoder是可以分开使用的,但是常常被结合使用以取得好的效果。
纵向分析
CNN Encoder-Decoder
In a CNN, an encoder-decoder network typically looks like this (a CNN encoder and a CNN decoder):
This is a network to perform semantic segmentation of an image. The left half of the network maps raw image pixels to a rich representation of a collection of feature vectors. The right half of the network takes these features, produces an output and maps the output back into the “raw” format (in this case, image pixels).
RNN Encoder-Decoder
In an RNN, an encoder-decoder network typically looks like this (an RNN encoder and an RNN decoder):
This is a network to predict responses for incoming emails. The left half of the network encodes the email into a feature vector, and the right half of the network decodes the feature vector to produce word predictions.
**Mixed Style Encoder-Decoder **
Note that it is not necessary to use just CNN or just RNN for encoder and decoder. We can mix and match and use a CNN encoder with RNN decoder, or vice versa; any combination can be used which is suitable for the given task.
An example from a paper I recently implemented from scratch, Text-guided Attention Model for Image Captioning (T-ATT):
Look at the parts I have highlighted in red. The STV refers to Skip-Thought Vectors. STV in itself is an encoder-decoder architecture.
Sequence-to-Sequence
Sequence-to-sequence (seq2seq)* 模型,顾名思义,其输入是一个序列,输出也是一个序列,例如输入是英文句子,输出则是翻译的中文。2014 Google提出Sequence-to-sequence的概念(待考证),在这之前也有使用encoder-decoder来解决sequence2sequence任务的,比如Bengio在2014年的论文中提出,提供了一种崭新的RNN Encoder-Decoder算法,并且将其应用于机器翻译中。seq2seq 可以用在很多方面:机器翻译、QA 系统、文档摘要生成、Image Captioning (图片描述生成器)。
Example
对于下面这个简单的示例模型,分为encoder-encoder vector-encoder三个部分。

Encoder和Decoder都是一个由RNN堆叠而成的网络,其实Sequence2Sequence的结构主要是使用的encoder-to-decoder的架构。我觉得seq2seq和auto-encoder是encoder-decoder衍生出来的、针对不同任务的框架,Seq2Seq的主要特点就是输入和输出长度可以不一样,而auto-encoder就是为了对输入进行重建。
Attention
上面所提及的Encoder-Decoder模型是有弊端的:
- 随着输入信息长度的增加,由于向量长度固定,先前编码好的信息会被后来的信息覆盖,丢失很多信息(当使用RNN作为Encoder时,由于其长短期记忆能力的有限,当输入信息长度变大,信息丢失严重)。中间语义向量无法完全表达整个输入序列的信息。(this fixed-length context vector design is incapability of remembering long sentences.)//(2015年的文章Bahdanau et al., 2015就是针对这个问题的。The attention mechanism was born to help **memorize long source sentences** in neural machine translation(Bahdanau et al., 2015))。
- 而且,每个输入的贡献都是一样的。
因此,在很多方面都出现了改进的模型,包括以下方面:s
I consider the approach of reversing a sentence a “hack”. It makes things work better in practice, but it’s not a principled solution. Most translation benchmarks are done on languages like French and German, which are quite similar to English (even Chinese word order is quite similar to English). But there are languages (like Japanese) where the last word of a sentence could be highly predictive of the first word in an English translation. In that case, reversing the input would make things worse. So, what’s an alternative? Attention Mechanisms.//某些时候是不可行的
-
Using LSTM or GRU cells.
而Attention就是一种通用的方法,在这部分呢,就来学习一下Attention 的思想.
神经网络中的注意机制基于人类中发现的视觉注意机制:
Attention Mechanisms in Neural Networks are (very) loosely based on the visual attention mechanism found in humans. Human visual attention is well-studied and while there exist different models, all of them essentially come down to being able to focus on a certain region of an image with “high resolution” while perceiving the surrounding image in “low resolution”, and then adjusting the focal point over time.
在早期就有使用这种attention的思想,但是最近几年才在深度学习领域火起来,下面举一个机器翻译里面应用attention的例子。
Attention In Bahdanau et al., 2015
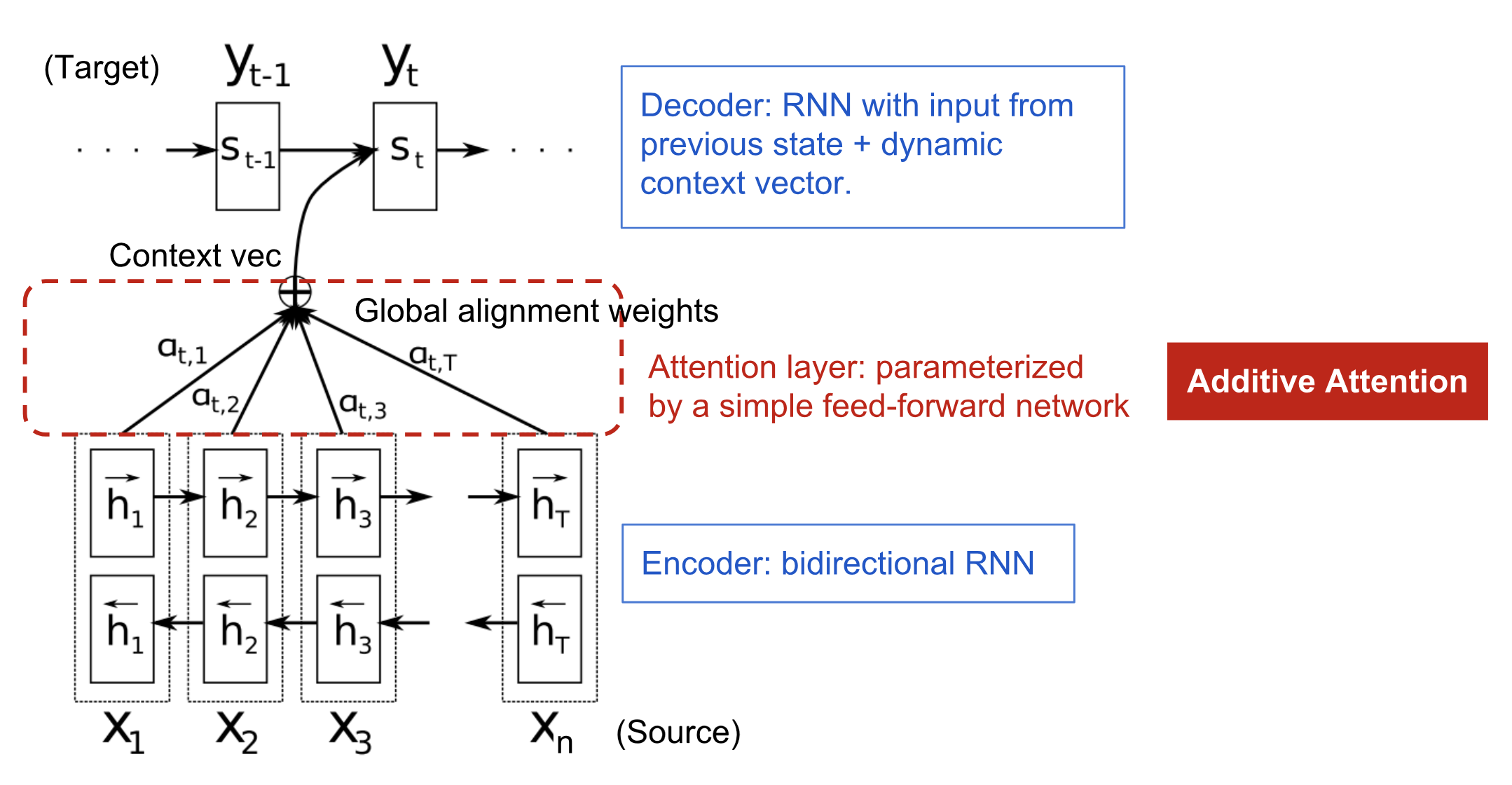
The encoder-decoder model with additive attention mechanism in [Bahdanau et al., 2015](https://arxiv.org/pdf/1409.0473.pdf). X为输入序列,y为预测序列,我们可以看到这个双向RNN的所有隐藏层输出被一个权重向量$\alpha$加权结合起来了,不再像以前一样,只使用最后一个隐藏层的输出:
The
are typically normalized to sum to 1 (so they are a distribution over the input states)
这个$\alpha$是一个矩阵,第t行($t=1……n$)表示$h_1,……,h_n$对$y_t$的输出所作的贡献,也就是说在decoder中,$y_{t-1}$和$\sum_{i=1}^n \alpha_{t,i} \boldsymbol{h}_i $作为t时刻Decoder的输入。
在这篇文章中,$\alpha$如何得到呢?通过一个单层隐藏层学得,$t$时刻$h_i$对$s_t$ or $y_t$的作用分数为: $V^T_a$和$W_a$都是待学习参数。以下就是学得的作用关系图,越亮,表示输入$x_i$对输出$y_j$的作用越大:

Alignment matrix of “L’accord sur l’Espace économique européen a été signé en août 1992” (French) and its English translation “The agreement on the European Economic Area was signed in August 1992”. (Image source: Fig 3 in Bahdanau et al., 2015) Attention or Memory
引入attention往往会引入新的计算代价,比如说处理上百的token sequence时,每个timestep输出的是h-dim的,那就会增加很多计算量:
Actually, that’s quite counterintuitive. Human attention is something that’s supposed to savecomputational resources. By focusing on one thing, we can neglect many other things. But that’s not really what we’re doing in the above model. We’re essentially looking at everything in detail before deciding what to focus on. Intuitively that’s equivalent outputting a translated word, and then going back through all of your internal memory of the text in order to decide which word to produce next. That seems like a waste, and not at all what humans are doing. In fact, it’s more akin to memory access,In this interpretation, instead of choosing what to “attend” to, the network chooses what to retrieve from memory. not attention, which in my opinion is somewhat of a misnomer (more on that below). Still, that hasn’t stopped attention mechanisms from becoming quite popular and performing well on many tasks.
An alternative approach to attention is to use Reinforcement Learning to predict an approximate location to focus to. That sounds a lot more like human attention, and that’s what’s done in Recurrent Models of Visual Attention.
Memory Mechanisms themselves have a much longer history……
Attention Family
With the help of the attention, the dependencies between source and target sequences are not restricted by the in-between distance anymore! Given the big improvement by attention in machine translation, it soon got extended into the computer vision field (Xu et al. 2015) and people started exploring various other forms of attention mechanisms (Luong, et al., 2015; Britz et al., 2017; Vaswani, et al., 2017).
Name Alignment score function Citation Content-base attention $\text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \text{cosine}[\boldsymbol{s}_t, \boldsymbol{h}_i]$ Graves2014 Additive(*) $\text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \mathbf{v}_a^\top \tanh(\mathbf{W}_a[\boldsymbol{s}_t; \boldsymbol{h}_i])$ Bahdanau2015 Location-Base $\alpha_{t,i} = \text{softmax}(\mathbf{W}_a \boldsymbol{s}_t)$
Note: This simplifies the softmax alignment to only depend on the target position.Luong2015 General $\text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \boldsymbol{s}_t^\top\mathbf{W}_a\boldsymbol{h}_i$
where $W_a$ is a trainable weight matrix in the attention layer.Luong2015 Dot-Product $\text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \boldsymbol{s}_t^\top\boldsymbol{h}_i$ Luong2015 Scaled Dot-Product(^) $\text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \frac{\boldsymbol{s}_t^\top\boldsymbol{h}_i}{\sqrt{n}}$
Note: very similar to the dot-product attention except for a scaling factor; where n is the dimension of the source hidden state.(*) Referred to as “concat” in Luong, et al., 2015 and as “additive attention” in Vaswani, et al., 2017. (^) It adds a scaling factor $1/\sqrt{n}$, motivated by the concern when the input is large, the softmax function may have an extremely small gradient, hard for efficient learning.
Attention分类
Name Definition Citation Self-Attention(&) Relating different positions of the same input sequence. Theoretically the self-attention can adopt any score functions above, but just replace the target sequence with the same input sequence. Cheng2016 Global/Soft Attending to the entire input state space. Xu2015 Local/Hard Attending to the part of input state space; i.e. a patch of the input image. Xu2015; Luong2015 (&) Also, referred to as “intra-attention” in Cheng et al., 2016 and some other papers.
接下来具体讲一些详细的Attention
Self-Attention
也叫intra-attention,在机器阅读、文章摘要、图像描述生成等领域很有用,也就是在同一个句子里面进行不同位置的attention,以在句子内部产生一个关联性信息的表达。
Soft vs Hard Attention
在 show, attend and tell 这篇文章中,提出soft\hard两种attention,不同在于两种attention所获取的信息不同,soft attention关注整张图像,而hard attention则关注图像部分区域,两者各有优势和劣势:
- soft:
- 优点:模型平滑、可微
- 缺点:当输入较大时,计算量大;
- hard
- 优势:在测试阶段计算量小
- 劣势:不可微,需要借助variance reduction 或 reinforcement learning来训练
Global vs. Local Attention
Luong, et al., 2015提出了两种attention,global attention类似于soft attention,而local attention是hard attentiond和soft attention的协调,它是可微的:
the model first predicts a single aligned position for the current target word and a window centered around the source position is then used to compute a context vector.
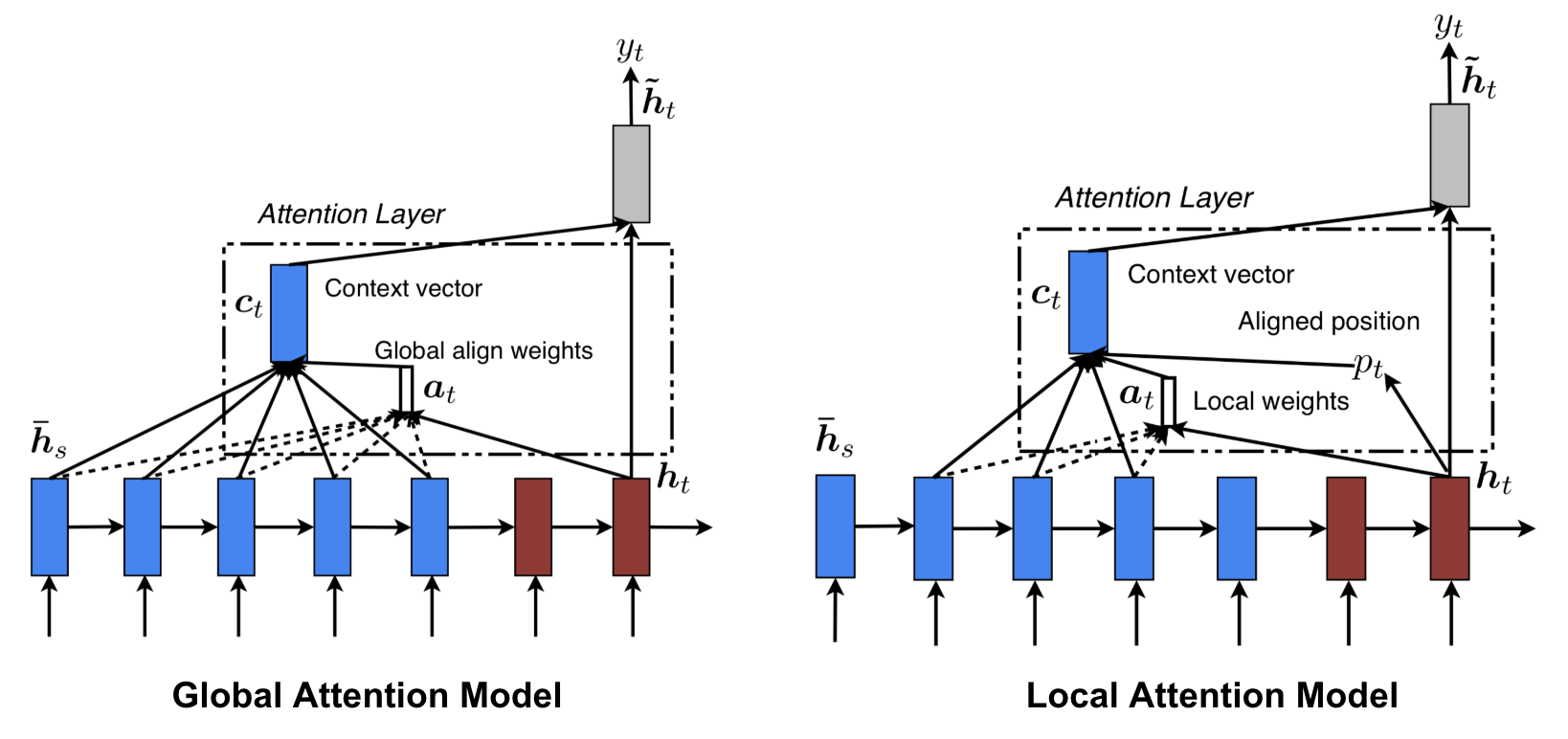
Global vs local attention (Image source: Fig 2 & 3 in Luong, et al., 2015) NMT
在介绍Transformer之前,我们介绍下NMT(Neural Turing Machines)。先来看下对Turing Machine的定义:
Alan Turing in 1936 proposed a minimalistic model of computation. It is composed of a infinitely long tape and a head to interact with the tape. The tape has countless cells on it, each filled with a symbol: 0, 1 or blank (“ “). The operation head can read symbols, edit symbols and move left/right on the tape. Theoretically a Turing machine can simulate any computer algorithm, irrespective of how complex or expensive the procedure might be. The infinite memory gives a Turing machine an edge to be mathematically limitless. However, infinite memory is not feasible in real modern computers and then we only consider Turing machine as a mathematical model of computation.

Fig. 9. How a Turing machine looks like: a tape + a head that handles the tape. (Image source: http://aturingmachine.com/)
再看下NTM的定义:
Neural Turing Machine (NTM, Graves, Wayne & Danihelka, 2014) is a model architecture for coupling a neural network with external memory storage. The memory mimics the Turing machine tape and the neural network controls the operation heads to read from or write to the tape. However, the memory in NTM is finite, and thus it probably looks more like a “Neural von Neumann Machine”.
NTM包含一个Controller和一个memory bank。前者可以是任何形式的神经网络,后者则是$N×M$的存储矩阵。Controller在处理操作的时候并行的访问memory,所有的读取写入操作都是结合soft attention进行的,也就是说都读或写的数据加上权重。
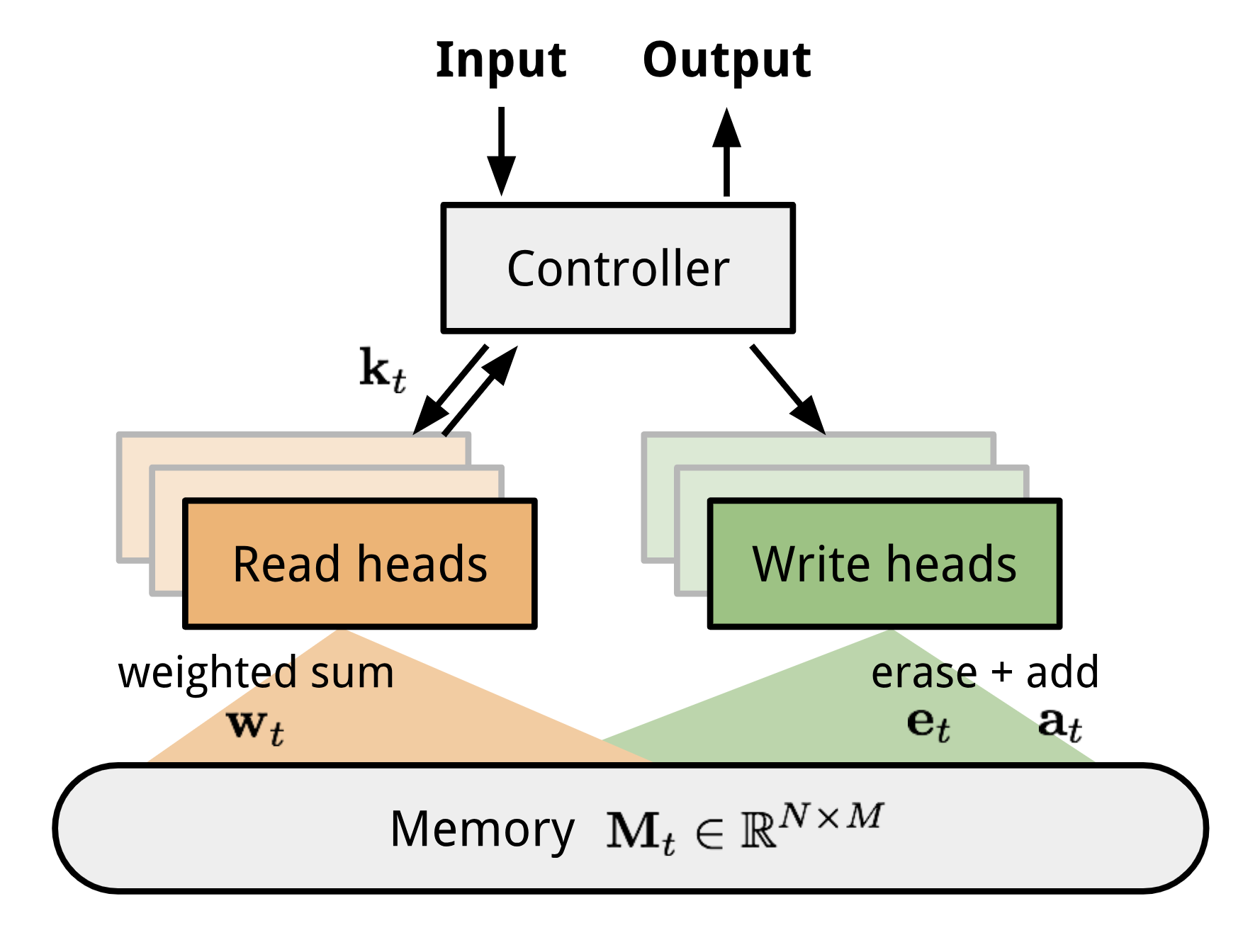
Fig 10. Neural Turing Machine Architecture.
读写操作
读取时,权重$w_t$控制对内存内容的行赋予权重: $w_t(i)$为第i个权重,$M_t(i)$为第i行内存向量。
写入时:
Attention机制
如何产生$w_t$呢?NTM使用了混合的 content-based 和location-based addressings。
Content-based addressing
Controller从input获得key vector $k_t$,计算它和memory row的cosine相似性,然后通过softmax进行归一化,另外引入$\beta_t$来放大或者缩小分布的关注重点:
Interpolation
计算了上步中的attention之后,我们结合上个timestep所产生的的 content-based attention计算最终的 content-based attention:
Location-based addressing
location-based addressing就是将attention vector中不同位置的值加权起来,具体就是通过允许整数移位的加权分布(a weighting distribution over allowable integer shifts)进行加权,它等价于卷积核(关于位置的偏移)为$s_t(·)$的一维卷积,有很多方式来定义这个分布:
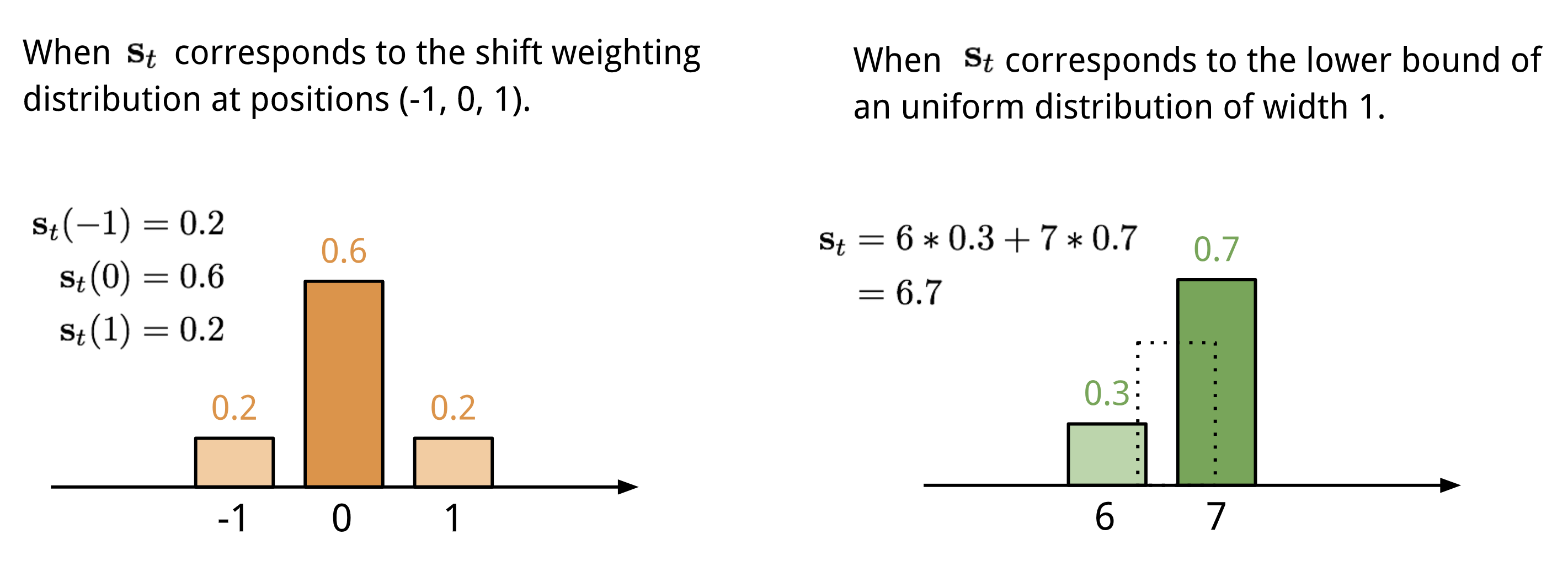
Two ways to represent the shift weighting distribution stst. 最终的attention经过$\gamma_t\ge1$来加强锐化: 整个产生$w_t$的过程如下所示,如果有并行的read和write操作,则controller将产生多组输出:
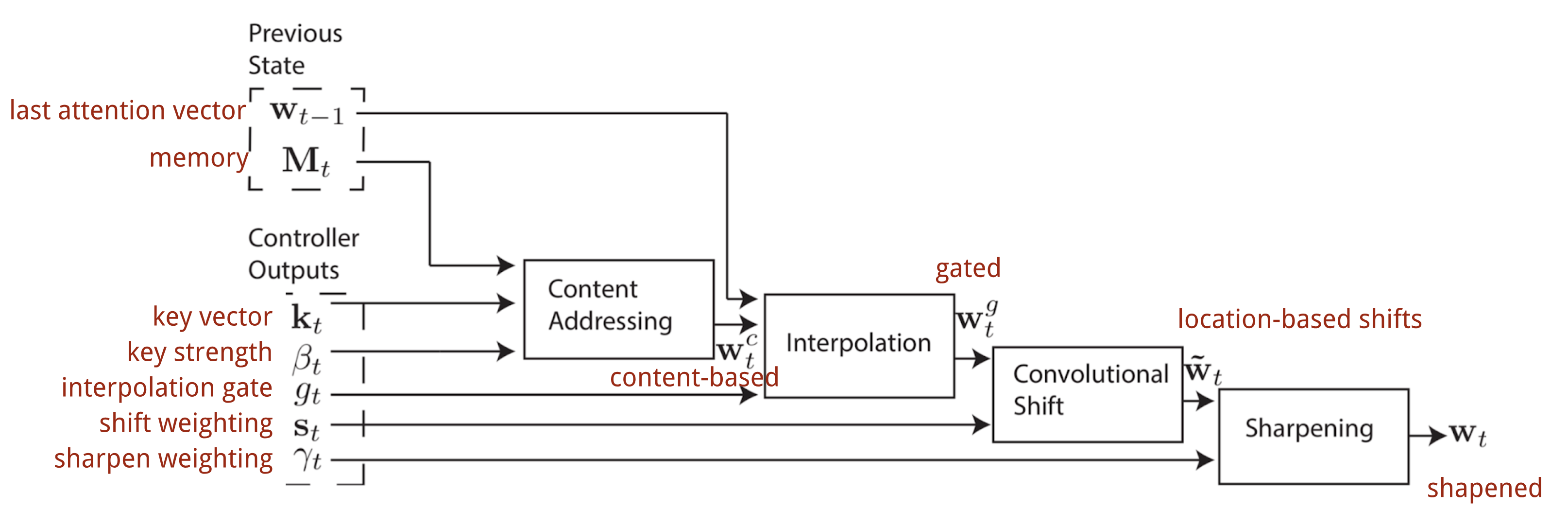
Fig. 12. Flow diagram of the addressing mechanisms in Neural Turing Machine. (Image source: Graves, Wayne & Danihelka, 2014) Transformer
Transformer是“Attention is All you Need” (Vaswani, et al., 2017)提出的一中soft attention,它使得不使用RNN units进行seq2seq的任务解决成为可能,Transformer模型完全建立在self-attention机制之上,并使用sequence-aligned recurrent architecture。这个模型最初是为了提高机器翻译的效率,因为RNN是顺序执行的,t时刻没有完成就不能处理t+1时刻,因此很难并行,但Transformer的Self-Attention机制和Position Encoding可以替代RNN,从而实现效率。后来发现Self-Attention效果很好,在很多其它的地方也可以使用Transformer模型。这包括著名的OpenAI GPT和BERT模型,都是以Transformer为基础的。当然它们只使用了Transformer的Decoder部分,由于没有了Encoder,Decoder只有Self-Attention而没有普通的Attention。
Key, Value and Query
主要组件是multi-head self-attention mechanism部分,它将输入和其编码表达看成key-value(K-V)对,且维度都是序列长度$n$。根据神经机器翻译的思想,(K,V)就是encoder 的隐藏状态;上一个输出被压缩成一个query(Q, m-dim),那么下一个输出,其实就是对(K,V,Q)的一个映射。
这里使用的attention是 前面表中scaled dot-product attention,针对V进行加权:
Multi-Head Self-Attention
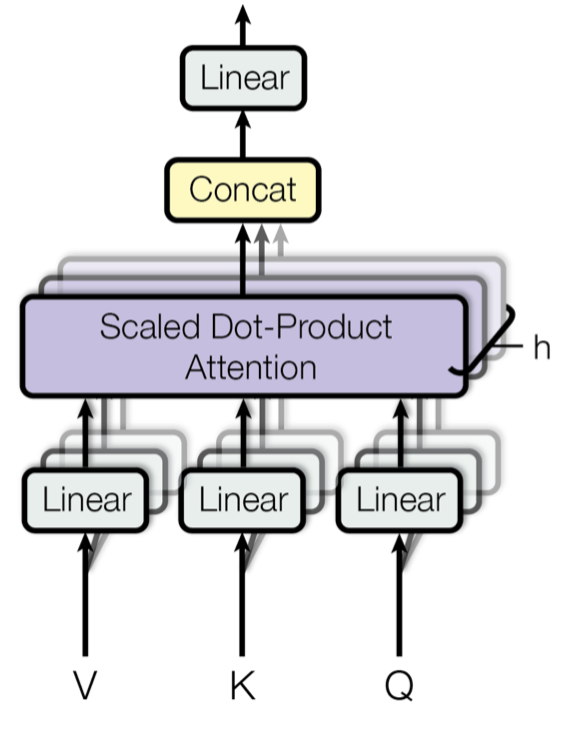
Fig. 14. Multi-head scaled dot-product attention mechanism. (Image source: Fig 2 in Vaswani, et al., 2017) 主要思想就是并行的运行这个scaled dot-product attention多次,然后拼接之后通过线性变换获取最终的attention,根据论文描述:
“multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.”
公式为: $W_i^Q,W_i^K,W_i^V,W^O$都是需要学习的参数。
Encoder
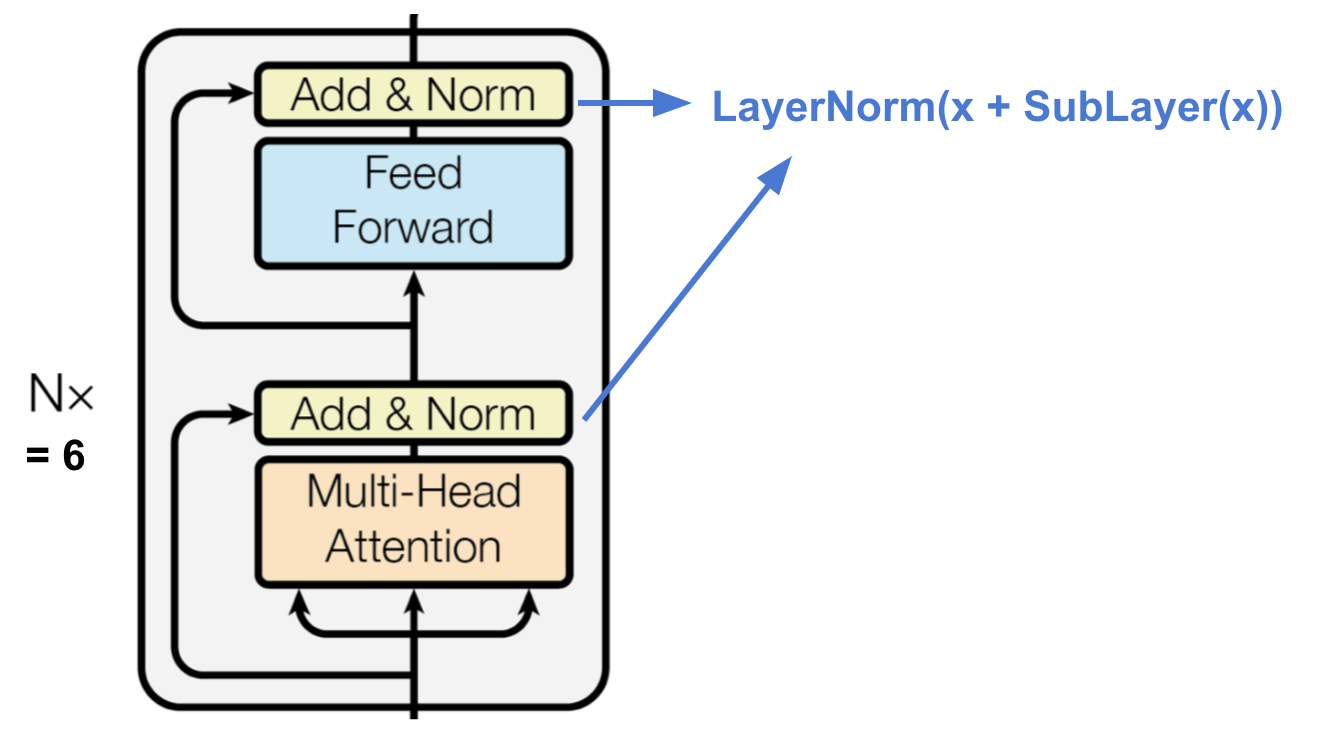
Fig. 15. The transformer’s encoder. (Image source: Vaswani, et al., 2017) encoder产生attention-based表示
- 6个等同的层
- 每层有一个multi-head self-attention layer和一个全连接层(feed forward)
- 每个子层都采用残差链接,以及层归一化操作,输出维度均为512-dim
Decoder
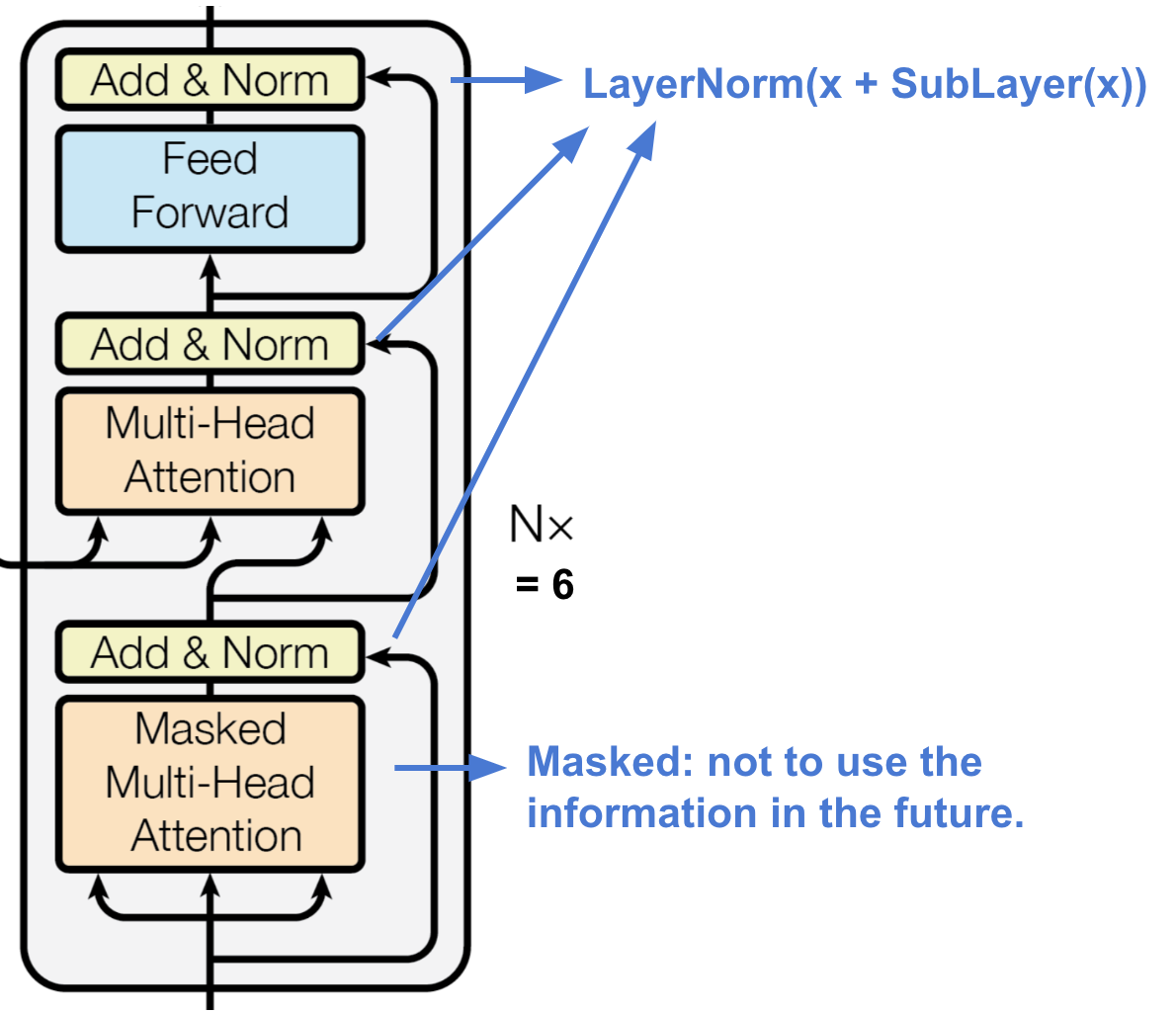
The transformer’s decoder. (Image source: Vaswani, et al., 2017) decoder通过使用context的信息,恢复或者产生想要的东西,结构描述:
-
6个等同层
-
每层两个子层,都使用multi-head self-attention layer,其中一个子层连接着一个全连接层
-
子层都有残差连接以及归一化操作
-
每层的第一个multi-head self-attention layer加了mask
The first multi-head attention sub-layer is modified to prevent positions from attending to subsequent positions, as we don’t want to look into the future of the target sequence when predicting the current position.
整个Transformer结构
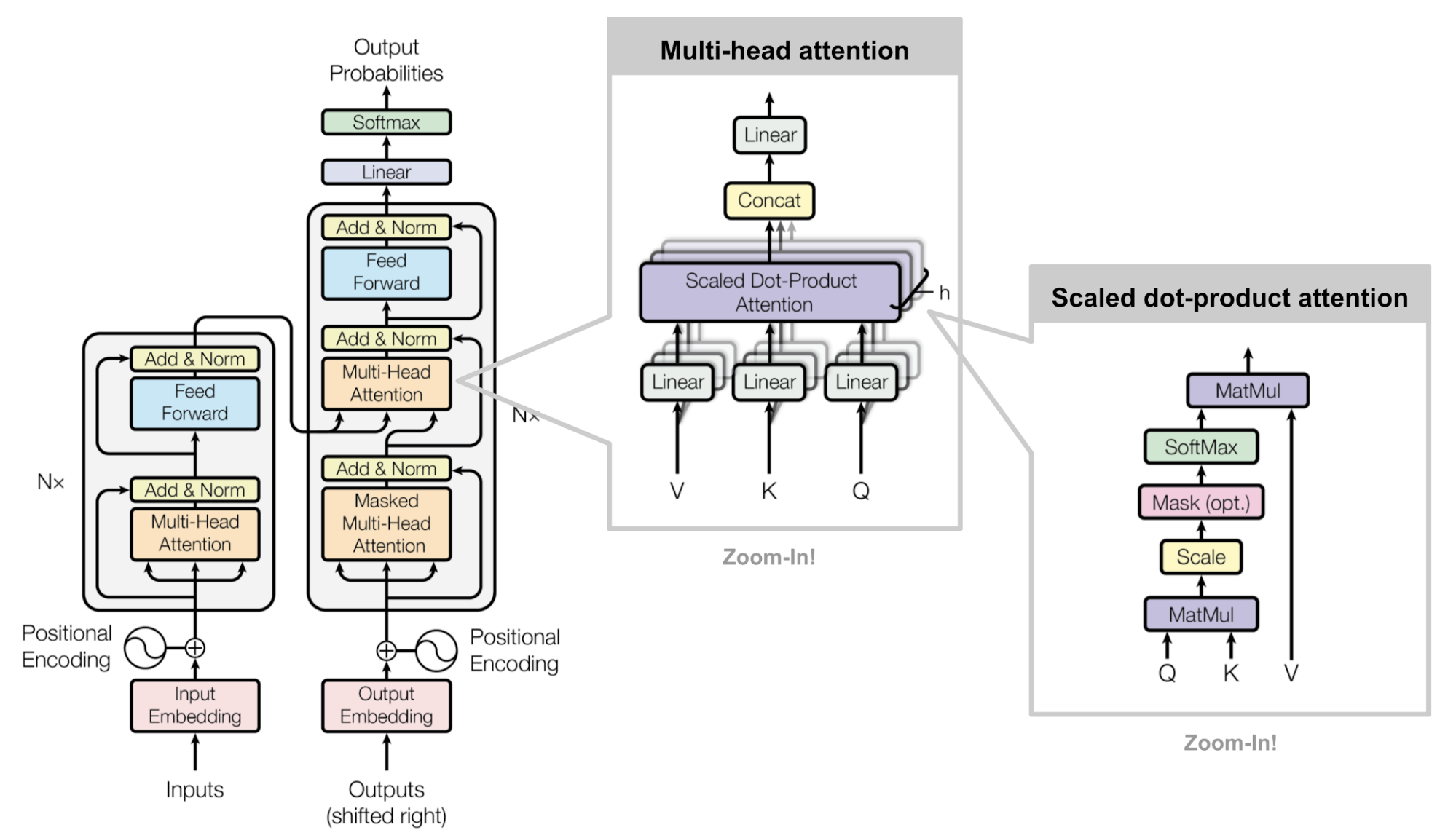
The full model architecture of the transformer. (Image source: Fig 1 & 2 in Vaswani, et al., 2017.) Referrence
感谢下面的文章博客等,文章有些部分是中英文混合的,一个原因是怕翻译不正确,另一个原因是内容太多,偷了点懒……
https://lilianweng.github.io/lil-log/2018/06/24/attention-attention.html#summary
https://towardsdatascience.com/understanding-encoder-decoder-sequence-to-sequence-model-679e04af4346
https://arxiv.org/pdf/1409.3215.pdf?source=post_page—————————
https://caicai.science/2018/10/06/attention%E6%80%BB%E8%A7%88/
http://www.wildml.com/2016/01/attention-and-memory-in-deep-learning-and-nlp/?source=post_page—————————
-
十大排序算法(一)-堆排序
理解
堆分为最大堆和最小堆,这里以最大堆为例子进行讲解。

堆的概念:
堆(英语:Heap)是计算机科学中的一种特别的树状数据结构。若是满足以下特性,即可称为堆:“给定堆中任意节点 P 和 C,若 P 是 C 的母节点,那么 P 的值会小于等于(或大于等于) C 的值”。若母节点的值恒小于等于子节点的值,此堆称为最小堆(英语:min heap);反之,若母节点的值恒大于等于子节点的值,此堆称为最大堆(英语:max heap)。在堆中最顶端的那一个节点,称作根节点(英语:root node),根节点本身没有母节点(英语:parent node)。
n个元素序列${k_1, k_2… k_i…k_n}$,当且仅当满足下列关系时称之为堆: $(k_i <= k_{2i}, k_i <= k_{2i+1)}$或者$(k_i >= k_{2i}, k_i >= k_{2i+1}), (i = 1, 2, 3, 4… n/2)$
在队列中,调度程序反复提取队列中第一个作业并运行,因为实际情况中某些时间较短的任务将等待很长时间才能结束,或者某些不短小,但具有重要性的作业,同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。[1] ~维基百科
堆排序
基本操作
操作 描述 时间复杂度 build 创建一个空堆 $O(n)$ insert 向堆中插入一个新元素 $O(log n)$ get 获取当前堆顶元素的值 $O(1)$ delete 删除堆顶元素 $O(\log n) $ 性质

堆一般用数组或者vector来存储,通过索引的操作虚拟一个完全二叉树结构。其性质有:
- 任意节点小于(或大于)它的所有后裔,最小元(或最大元)在堆的根上(堆序性)。
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
常见的堆有二叉堆、斐波那契堆等。
原理
虽然理论容易理解,但是要真正把这个算法搞通,包括能直接手写算法,在实现的时候还是会觉得有一点难度。这里需要谨记的是 给定一个根节点, 若其左子树和右子树同时满足堆的条件后,对根节点完成下沉操作后,整个树🌲一定是一个堆。
完全二叉树的节点索引关系 假设有一个数组从1开始的size为n的数组arr。其最后一个非叶子节点的索引为$start=(n/2)$,该非叶子节点的左儿子为$start2$,右儿子为$start2+1$;注意,若数组从0开始,其最后一个非叶子节点的索引为$start=(n/2-1)$,该非叶子节点的左儿子为$start2+1$,右儿子为$start2+2$,以下部分,包括实现,都是从0开始的。
基本操作
这里只解说,几个比较难的操作。
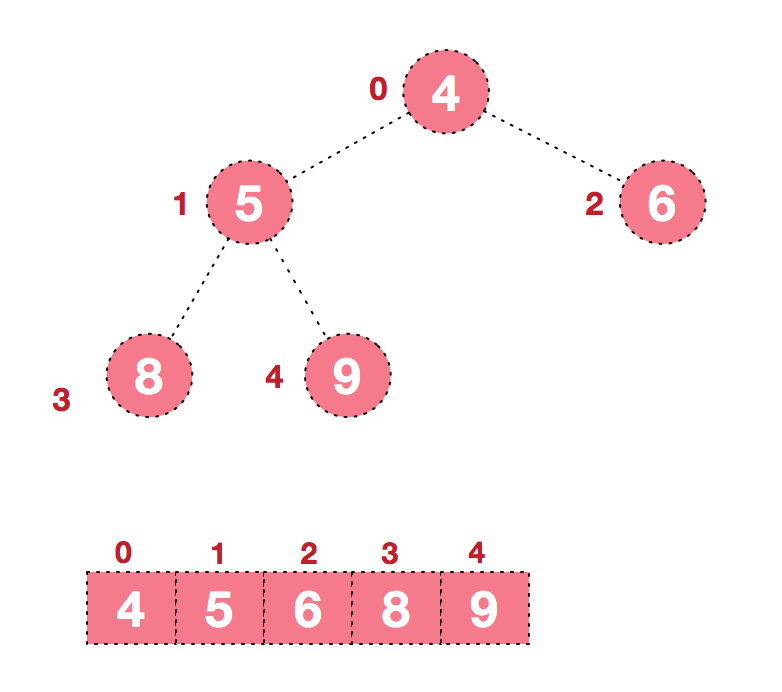
第一步:build-构建最大堆
给定一个输入数组,可以得到如下的一个初始完全二叉树
 为了得到一个堆,build操作需要从这个二叉树的最后一个非叶子节点开始,对所有的非叶子节点进行下沉操作,也就是MaxHeap构造函数中下面的代码:
为了得到一个堆,build操作需要从这个二叉树的最后一个非叶子节点开始,对所有的非叶子节点进行下沉操作,也就是MaxHeap构造函数中下面的代码:int curPos=size/2-1;//最后一个非叶子节点 while(curPos>=0)//循环下沉所有叶子节点 { shift_down(curPos,arrSize-1);//下沉操作 curPos--;//非叶子节点的位置 }最终得到这样一个堆:
下沉 这个地方需要讲解一下下沉操作。下沉每个节点的时候,都要保证其做子树和右子树都是一个堆,这也是为什么构建堆时,下沉操作是从最后一个非叶子节点开始的。我们再回忆前面的关键概念:给定一个树的根节点, 若其左子树和右子树同时满足堆的条件后,对根节点完成下沉操作后,整个树🌲一定是一个堆。
下沉操作是通过一个循环来实现的,循环是为了保证下沉能够完全进行,也就是说有可能下沉一次,交换了两个节点的值,会导致子树不再满足堆的性质,这个时候,这个节点还需要继续下沉。也就是下面的例子:4要下沉两次。
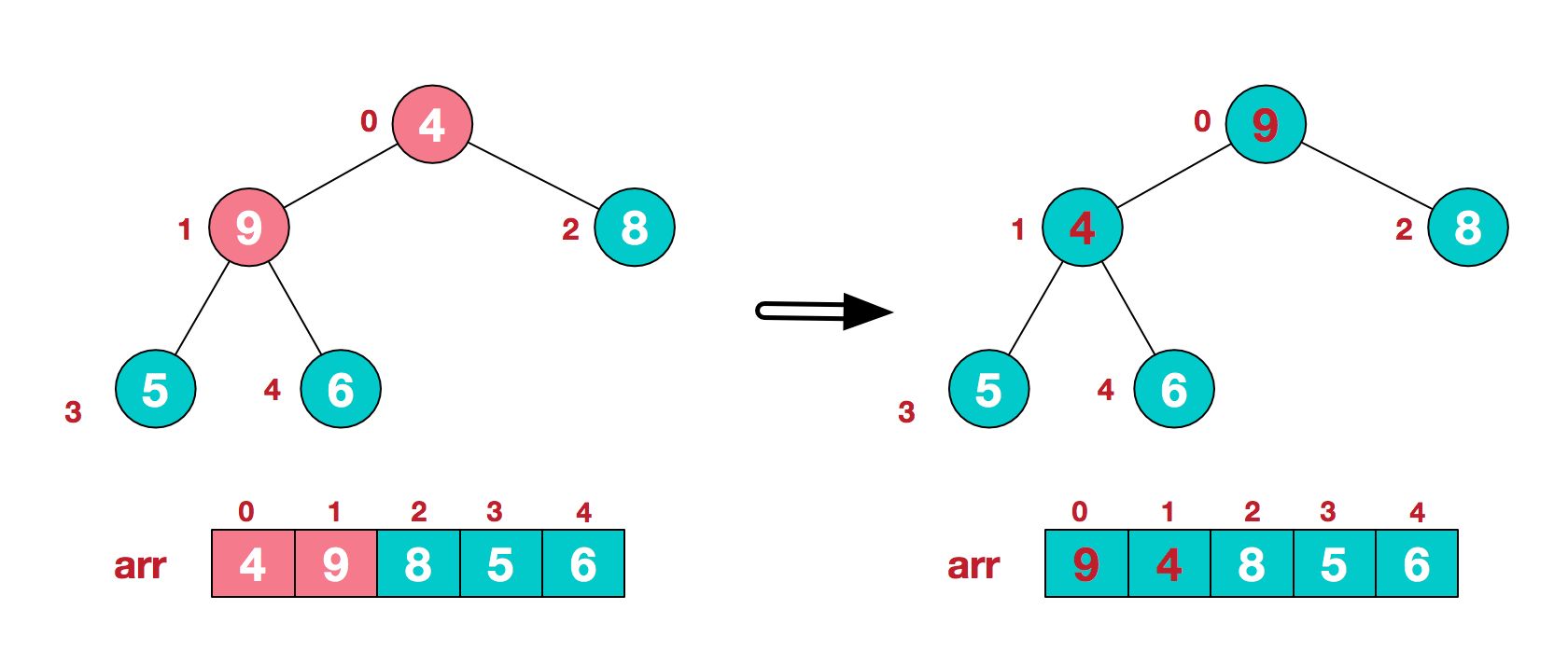

T temp=heap[i];//当前非叶子节点 while (j<=end)//是否继续进行往下沉的条件 { if(j+1<end&&heap[j]>heap[j+1])//找到两个儿子节点更大的一个 { j++; } if(temp<heap[j])break;//表示此节点i已经满足堆的条件,不需要继续往下沉; //否则,会继续往下判断 heap[i]=heap[j]; i=j;//新的节点 j=2*j+1;//新节点的左子节点 } heap[i]=temp;//完成两个节点的交换,也可能是heap[i]和自身的赋值,比如在while循环的第一遍循环就break出去。这个地方还需要注意的是对新的非叶子节点索引的计算以及左儿子索引非计算。
堆的插入和删除操作
堆构建完成后,我们可以进行插入和删除操作,插入操作的思想就是讲元素插入到堆的末尾,也就是数组的末尾,堆的尺寸加1,然后对这个末尾的新元素进行上浮操作,也就是说一直向上移动该元素,直到其父节点大于该元素。若插入前,该数组的大小为size,那么新元素的父节点索引就是$i=(size-1)/2$,若一次上浮无法满足堆的性质,就计算新的父节点i=$(i-1)/2$。
T temp=heap[j]; while (j>=0) { if(temp<heap[i])//插入的时候就已经满足堆的条件,则不需要再继续上浮了 { break; } else {//插入时不满足,上浮 heap[j]=heap[i]; } j=i;//j指向其父节点 i=(i-1)/2;//j为新j的父节点 } heap[j]=temp;//完成交换对于删除操作呢,就比较简单了,就是交换堆顶元素和最后一个元素的值,堆的尺寸减1,然后对根节点进行下沉操作即可,因为我们要时刻记得:给定一个树的根节点, 若其左子树和右子树同时满足堆的条件后,对根节点完成下沉操作后,整个树🌲一定是一个堆。所以删除操作就没有什么复杂的操作了。
堆排序实现
要注意空堆和堆容量的判断,还有堆的尺寸要注意改变。
基类
#ifndef SORT_HEAP_H #define SORT_HEAP_H enum{DEFAUKT_SIZE=10}; template <typename T> class Heap { public: Heap()=default; virtual ~Heap()= default; virtual void show_heap()const =0; virtual bool insert_heap(const T&)=0; virtual bool remove_heap(T&)=0; }; #endif //SORT_HEAP_H最大堆
头文件
#ifndef SORT_MAXHEAP_H #define SORT_MAXHEAP_H #include "heap.h" template <typename T> class MaxHeap: public Heap<T> { public: /** * 创建一个空堆 */ MaxHeap(int sz=DEFAUKT_SIZE); /** * 根据已有数组堆创建一个堆 */ MaxHeap(const T[],const int ); /** * 析构函数 */ ~MaxHeap(); /** * 显示堆 */ void show_heap()const; /** * 向堆中插入元素 * @return */ bool insert_heap(const T&); /** * 移除堆中的元素 * @return */ bool remove_heap(T&); protected: /** * 下浮 */ void shift_down(int,int); /** * 上浮 */ void shift_up(int); private: //指向堆的指针 T *heap; //已有堆中元素个数 int size; //堆的容量 int capacity; }; #endif //SORT_MAXHEAP_Hcpp文件
#include <form.h> #include "MaxHeap.h" template <typename T> MaxHeap<T>::MaxHeap(int sz) { capacity=sz>DEFAUKT_SIZE?sz:DEFAUKT_SIZE; heap=new T[capacity]; assert(heap!= nullptr); size=0; } template <typename T> MaxHeap<T>::MaxHeap(const T arr[],const int arrSize) { capacity=arrSize>DEFAUKT_SIZE?arrSize:DEFAUKT_SIZE; heap=new T[capacity]; size=arrSize; for(int i=0;i<arrSize;i++) { heap[i]=arr[i]; } int curPos=size/2-1; while(curPos>=0) { shift_down(curPos,arrSize-1); curPos--; } } template <typename T> void MaxHeap<T>::shift_down(int start, int end) { int i=start;//第i个非叶子节点 int j=start*2+1;//第i个非叶子节点的左儿子 T temp=heap[i]; while (j<=end)//是否继续进行往下沉的条件 { if(j+1<end&&heap[j]>heap[j+1])//找到两个儿子节点更大的一个 { j++; } if(temp<heap[j])break;//表示此节点i已经满足堆的条件,不需要继续往下沉; //否则,会继续往下判断 heap[i]=heap[j]; i=j;//新的节点 j=2*j+1;//新节点的左子节点 } heap[i]=temp;//完成两个节点的交换,也可能是heap[i]和自身的赋值,比如在while循环的第一遍循环就break出去。 } template <typename T> MaxHeap<T>::~MaxHeap() { delete heap; heap= nullptr; capacity=size=0; } template <typename T> void MaxHeap<T>::shift_up(int e) { int j=e;//j为最后新加入的元素 int i=(e-1)/2;//j的父节点 T temp=heap[j]; while (j>=0) { if(temp<heap[i])//插入的时候就已经满足堆的条件 { break; } else {//插入时不满足 heap[j]=heap[i]; } j=i;//j指向其父节点 i=(i-1)/2;//j为新j的父节点 } heap[j]=temp;//完成交换 } template<typename T> bool MaxHeap<T>::insert_heap(const T &val) { if(size>=capacity)return false; heap[size]=val; shift_up(size); size+=1; return true; } template <typename T> bool MaxHeap<T>::remove_heap(T &val) { if(size<=0)return false; val=heap[0]; heap[0]=heap[size-1]; --size; shift_down(0,size-1);//这里root就是数组的第一个元素。 // 所以从0开始;而在初始建堆的时候是从最后一个非叶子节点开始下沉的, // 这样是为了保证在下沉每个节点时,其左右子树都满足堆的条件。 }参考资料:
代码实现:https://blog.csdn.net/FreeeLinux/article/details/52162788
理论理解:https://www.cnblogs.com/chengxiao/p/6129630.html
-
[转]论文阅读:Semi-Supervised Classification with Graph Convolutional Networks
思想
GCN 是谱图卷积(spectral graph convolution) 的局部一阶近似(localized first-order approximation)。GCN的另一个特点在于其模型规模会随图中边的数量的增长而线性增长。总的来说,GCN 可以用于对局部图结构与节点特征进行编码。
特点
图卷积神经网络具有几个特点:
- 局部特性:图卷积神经网络关注的是图中以某节点为中心,K阶邻居之内的信息,这一点与GNN有本质的区别;
- 一阶特性:经过多种近似之后,GCN变成了一个一阶模型。也就是说,单层的GCN可以被用于处理图中一阶邻居上的信息;若要处理K阶邻居,可以采用多层GCN来实现;
- 参数共享:对于每个节点,其上的滤波器参数 W 是共享的,这也是其被称作图卷积网络的原因之一。
Symbols
- $\mathcal{G}=(\mathcal{V},\mathcal{E}) $表示一个图, $\mathcal{V},\mathcal{E} $分别表示相应的节点集与边集,$u,v\in\mathcal{V} $表示图中的节点,$ (u,v)\in\mathcal{E} $表示图中的边。
- A 表示图的邻接矩阵(adjacency matrix)。节点的连接情况的矩阵。该矩阵可以是二值的,也可以是带权的
- D 表示图的度矩阵(degree matrix)。度矩阵是一个对角矩阵,对于无向图来说,一般只使用入度矩阵或出度矩阵。
- L 表示图的拉普拉斯矩阵(Laplacian matrix),$\mathcal{L}$ 表示图的归一化拉普拉斯矩阵。

-
graph convolutional network思想简介
注:https://zhuanlan.zhihu.com/p/37091549,这篇blog写的很好,我借鉴其关键内容并重新整理了一下,添加了一些自己的看法。
为什么有图卷积网络
卷积神经网络的缺点:它研究的对象还是限制在Euclidean domains的数据。什么是euclidean data? Euclidean data最显著的特征就是有规则的空间结构,比如图片是规则的正方形栅格,比如语音是规则的一维序列。而这些数据结构能够用一维、二维的矩阵表示,卷积神经网络处理起来很高效。
- RNN原理、公式推导及python实现
- Word Embedding models的深入理解
- 从EncoderDecoder到Transformer
- 十大排序算法(一)-堆排序
- [转]论文阅读:Semi-Supervised Classification with Graph Convolutional Networks
- graph convolutional network思想简介
- 0/1背包问题
- 自平衡二叉搜索树
- relation network for object detection
- Deep Visual-Semantic Alignments for Generating Image Description