原理
随机采样一致性(RANSAC)算法[40]根据一组包含异常数据的样本,估计出这组数据满足的数学模型参数;假设符合数学模型的那点称为局内点,而不符合数学模型的那些点被称为局外点。随机采样一致性通过反复的选择数据中的一组数据子集来达成目标,被选取的数据子集初始为局内点,并通过迭代求解最优结果。在模型确定情况下,以及最大迭代次数是允许的情况下,随机采样一致性算法总是能够找到最优解。


随机采样一致性算法的输入是
- 一组观测点,其中包含局内点与局外点;
- 提供一个可以由数据拟合的模型,含有未知参数;
- 判断为一个模型所需要的最小数据量;
- 算法的迭代的最大次数;
- 阈值,这个阈值限定什么时候数据点能够满足模型;邻近数据值得数量,用来判断模型是否能和数据进行很好的拟合。
RANSAC的应用
Calculate Homography: A homography can be computed when we have 4 or more corresponding points in two images. Automatic feature matching explained in the previous section does not always produce 100% accurate matches. It is not uncommon for 20-30% of the matches to be incorrect. Fortunately, the findHomography method utilizes a robust estimation technique called Random Sample Consensus (RANSAC) which produces the right result even in the presence of large number of bad matches.
c++ // Extract location of good matches std::vector<Point2f> points1, points2; for( size_t i = 0; i < matches.size(); i++ ) { points1.push_back( keypoints1[ matches[i].queryIdx ].pt ); points2.push_back( keypoints2[ matches[i].trainIdx ].pt ); } // Find homography h = findHomography( points1, points2, RANSAC );
与标准最小二乘法拟合直线比较:
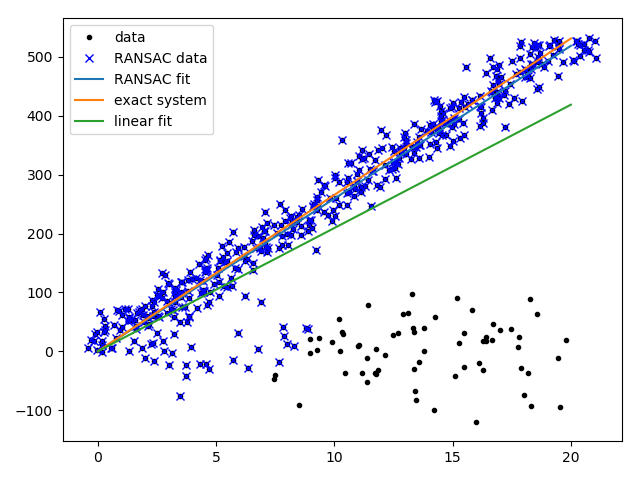
RANSAC的实现: 采用最小二乘法来作为模型拟合群内点:
import numpy
import scipy # use numpy if scipy unavailable
import scipy.linalg # use numpy if scipy unavailable
def ransac(data, model, n, k, t, d, debug=False, return_all=False):
#######
"""fit model parameters to data using the RANSAC algorithm
This implementation written from pseudocode found at
http://en.wikipedia.org/w/index.php?title=RANSAC&oldid=116358182
Given:
data - a set of observed data points
model - a model that can be fitted to data points
n - the minimum number of data values required to fit the model
k - the maximum number of iterations allowed in the algorithm
t - a threshold value for determining when a data point fits a model
d - the number of close data values required to assert that a model fits well to data
Return:
bestfit - model parameters which best fit the data (or nil if no good model is found)
iterations = 0
bestfit = nil
besterr = something really large
while iterations < k {
maybeinliers = n randomly selected values from data
maybemodel = model parameters fitted to maybeinliers
alsoinliers = empty set
for every point in data not in maybeinliers {
if point fits maybemodel with an error smaller than t
add point to alsoinliers
}
if the number of elements in alsoinliers is > d {
% this implies that we may have found a good model
% now test how good it is
bettermodel = model parameters fitted to all points in maybeinliers and alsoinliers
thiserr = a measure of how well model fits these points
if thiserr < besterr {
bestfit = bettermodel
besterr = thiserr
}
}
increment iterations
}
return bestfit
"""
##########
iterations = 0
bestfit = None
besterr = numpy.inf
best_inlier_idxs = None
while iterations < k:
maybe_idxs, test_idxs = random_partition(n, data.shape[0])
maybeinliers = data[maybe_idxs, :]
test_points = data[test_idxs]
maybemodel = model.fit(maybeinliers)
test_err = model.get_error(test_points, maybemodel)
also_idxs = test_idxs[test_err < t] # select indices of rows with accepted points
alsoinliers = data[also_idxs, :]
if debug:
print('test_err.min()', test_err.min())
print('test_err.max()', test_err.max())
print('numpy.mean(test_err)', numpy.mean(test_err))
print('iteration %d:len(alsoinliers) = %d' %(iterations, len(alsoinliers)))
if len(alsoinliers) > d:
betterdata = numpy.concatenate((maybeinliers, alsoinliers))
bettermodel = model.fit(betterdata)
better_errs = model.get_error(betterdata, bettermodel)#重新计算总的error
thiserr = numpy.mean(better_errs)
if thiserr < besterr:
bestfit = bettermodel
besterr = thiserr
best_inlier_idxs = numpy.concatenate((maybe_idxs, also_idxs))
iterations += 1
if bestfit is None:
raise ValueError("did not meet fit acceptance criteria")
if return_all:
return bestfit, {'inliers': best_inlier_idxs}
else:
return bestfit
def random_partition(n, n_data):
"""return n random rows of data (and also the other len(data)-n rows)"""
all_idxs = numpy.arange(n_data)
numpy.random.shuffle(all_idxs)
idxs1 = all_idxs[:n]
idxs2 = all_idxs[n:]
return idxs1, idxs2
class LinearLeastSquaresModel:
"""linear system solved using linear least squares
This class serves as an example that fulfills the model interface
needed by the ransac() function.
"""
def __init__(self, input_columns, output_columns, debug=False):
self.input_columns = input_columns
self.output_columns = output_columns
self.debug = debug
def fit(self, data):
A = numpy.vstack([data[:, i] for i in self.input_columns]).T
B = numpy.vstack([data[:, i] for i in self.output_columns]).T
x, resids, rank, s = numpy.linalg.lstsq(A, B)
return x
def get_error(self, data, model):
A = numpy.vstack([data[:, i] for i in self.input_columns]).T
B = numpy.vstack([data[:, i] for i in self.output_columns]).T
B_fit = scipy.dot(A, model)
err_per_point = numpy.sum((B - B_fit) ** 2, axis=1) # sum squared error per row
return err_per_point
def test():
# generate perfect input data
n_samples = 500
n_inputs = 1
n_outputs = 1
A_exact = 20 * numpy.random.random((n_samples, n_inputs))
perfect_fit = 60 * numpy.random.normal(size=(n_inputs, n_outputs)) # the model
B_exact = scipy.dot(A_exact, perfect_fit)
assert B_exact.shape == (n_samples, n_outputs)
# add a little gaussian noise (linear least squares alone should handle this well)
A_noisy = A_exact + numpy.random.normal(size=A_exact.shape)
B_noisy = B_exact + numpy.random.normal(size=B_exact.shape)
if 1:
# add some outliers
n_outliers = 100
all_idxs = numpy.arange(A_noisy.shape[0])
numpy.random.shuffle(all_idxs)
outlier_idxs = all_idxs[:n_outliers]#制造outliers
non_outlier_idxs = all_idxs[n_outliers:]
A_noisy[outlier_idxs] = 20 * numpy.random.random((n_outliers, n_inputs))
B_noisy[outlier_idxs] = 50 * numpy.random.normal(size=(n_outliers, n_outputs))
# setup model
all_data = numpy.hstack((A_noisy, B_noisy))#(x,y)
input_columns = range(n_inputs) # the first columns of the array
output_columns = [n_inputs + i for i in range(n_outputs)] # the last columns of the array
debug = True
model = LinearLeastSquaresModel(input_columns, output_columns, debug=debug)
linear_fit, resids, rank, s = numpy.linalg.lstsq(all_data[:, input_columns], all_data[:, output_columns])
# run RANSAC algorithm
ransac_fit, ransac_data = ransac(all_data, model,5, 5000, 7e4, 50, # misc. parameters
debug=debug, return_all=True)
if 1:
import pylab
sort_idxs = numpy.argsort(A_exact[:, 0])
A_col0_sorted = A_exact[sort_idxs] # maintain as rank-2 array
if 1:
pylab.plot(A_noisy[:, 0], B_noisy[:, 0], 'k.', label='data')
pylab.plot(A_noisy[ransac_data['inliers'], 0], B_noisy[ransac_data['inliers'], 0], 'bx',
label='RANSAC data')
else:
pylab.plot(A_noisy[non_outlier_idxs, 0], B_noisy[non_outlier_idxs, 0], 'k.', label='noisy data')
pylab.plot(A_noisy[outlier_idxs, 0], B_noisy[outlier_idxs, 0], 'r.', label='outlier data')
pylab.plot(A_col0_sorted[:, 0],
numpy.dot(A_col0_sorted, ransac_fit)[:, 0],
label='RANSAC fit')
pylab.plot(A_col0_sorted[:, 0],
numpy.dot(A_col0_sorted, perfect_fit)[:, 0],
label='exact system')
pylab.plot(A_col0_sorted[:, 0],
numpy.dot(A_col0_sorted, linear_fit)[:, 0],
label='linear fit')
pylab.legend()
pylab.show()
if __name__ == '__main__':
test()