RNN的梯度消失、爆炸问题

在$t_0$时刻对于 $W_x,W_s$求偏导,并没有长期依赖,但是会随着时间序列产生长期依赖。因为 随着时间序列向前传播,而
又是 的函$W_x,W_s$数。对于$t_3$时刻:

求导数:
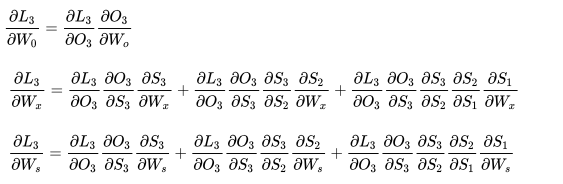
归纳:
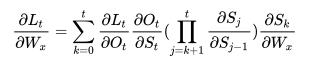
加上激活函数,得到递归导数:
As shown in this paper, if the dominant eigenvalue of the matrix $W_s$ is greater than 1, the gradient explodes. If it is less than 1, the gradient vanishes.The fact that this equation leads to either vanishing or exploding gradients should make intuitive sense. Note that the values of $f′(x)$will always be less than 1. So if the magnitude of the values of$W_s$ are too small, then inevitably the derivative will go to 0. The repeated multiplications of values less than one would overpower the repeated multiplications of $W_s$ . On the contrary, make $W_s$ too big and the derivative will go to infinity since the exponentiation of WRWR will overpower the repeated multiplication of the values less than 1. In practice, the vanishing gradient is more common, so we will mostly focus on that.
According to the above math, if the gradient vanishes it means the earlier hidden states have no real effect on the later hidden states, meaning no long term dependencies are learned!(就是说没学到长期依赖,很远层的权重不受早期层的什么影响)
梯度问题的根源就在这个公式,因为$tanh’\leq1$,对于训练过程大部分情况下tanh的导数是小于1的,
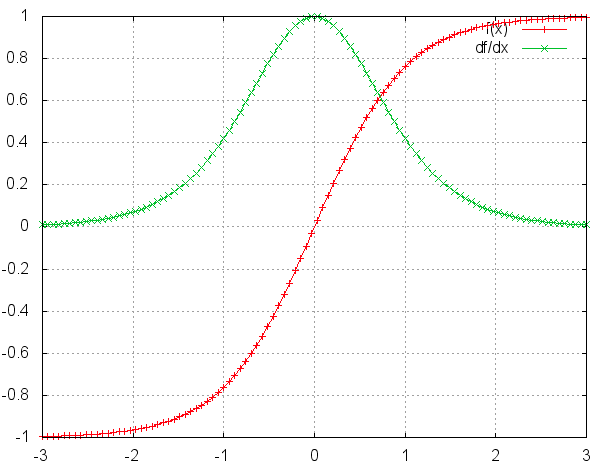
因为很少情况下会出现,而$W_s$ 的值也可能出现很大值或很小值。如果
也是一个大于0小于1的值,则当t很大时
,就会趋近于0,同理当
很大时
就会趋近于无穷,这就是RNN中梯度消失和爆炸的原因。要消除这种情况就需要把这一坨在求偏导的过程中去掉,至于怎么去掉,一种办法就是使递归导数
另一种办法就是使递归导数
。其实这就是LSTM做的事情
分析论文有 http://www.bioinf.jku.at/publications/older/2604.pdf、https://arxiv.org/pdf/1211.5063.pdf
LSTM解决Naive RNN的梯度消失、爆炸问题
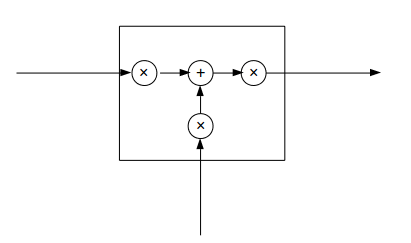
RNN结构可以抽象成下面这幅图:

为什么不用relu代替tanh来解决RNN的梯度消失问题呢?
换成ReLU在一定程度上可以解决梯度消失的问题,但是在RNN中直接把激活函数换成ReLU会导致非常大的输出值。将tanh换成ReLU,最后计算的结果会变成多个W连乘,如果W中存在特征值>1的,那么经过BPTT连乘后得到的值会爆炸,产生梯度爆炸的问题,使得RNN仍然无法传递较远距离。因此,RNN没办法BPTT较远的距离的原因就是如此
可参看A Simple Way to Initialize Recurrent Networks of Rectified Linear Units
LSTM:解决梯度消失问题
Lstm cell图及公式
- LSTM的可以抽象成这样一幅图:
-
详细结构

LSTM解决梯度消失的原理
通俗地讲:RNN中,每个记忆单元$s_t-1$都会乘上一个W和激活函数的导数,这种连乘使得记忆衰减的很快。所有“gradient based”的方法在权重更新都会遇到两个问题:input weight conflict 和 output weight conflict。大意就是对于神经元的权重 ,不同的数据 所带来的更新是不同的,这样可能会引起冲突(比如有些输入想让权重变小,有些想让它变大)。网络可能需要选择性地“忘记”某些输入,以及“屏蔽”某些输出以免影响下一层的权重更新。为了解决这些问题,LSTM引入了3个门。
早期LSTM
在早期的LSTM中,是让这个递归导数有常量值,这样就不会出现梯度消失或者爆炸。就是强行让 error flow 变成一个常数: $w_{jj}$就是RNN里自己到自己的连接。他们把这样得到的模块叫做CEC(constant error carrousel),很显然由于上面那个约束条件的存在,这个CEC模块是线性的。而LSTM把原本RNN的单元改造成一个叫做CEC的部件,这个部件保证了误差将以常数的形式在网络中流动 ,并在此基础上添加输入门和输出门使得模型变成非线性的,并可以调整不同时序的输出对模型后续动作的影响。通过记忆和当前输入”相加”,使得之前的记忆会继续存在而不是受到乘法的影响而部分“消失”,因此不会衰减。 在这个公式中,递归导数项的导数是1,就不会出现梯度问题。The reason for this is because, in order to enforce this constant error flow, the gradient calculation was truncated so as not to flow back to the input or candidate gates. So with respect to $C_{t−1}$ they could be treated as constants. Here what they say in the original paper:
However,to ensure non-decaying error backprop through internal states of memory cells, as with truncated BPTT (e.g.,Williams and Peng 1990), errors arriving at “memory cell net inputs” [the cell output, input, forget, and candidate gates] …do not get propagated back further in time (although they do serve to change the incoming weights).Only within memory cells [the cell state],errors are propagated back through previous internal states.
Modern LSTM
早期的公式并不是很好,因为$C_t$的增长是没办法控制的,为了限制无限制的增长,一个忘记门提出来了,用来控制cell state.很多现有的解释也不是基于现在这个完整公式的,也就是递归导数公式等于 $f$.现在基于这个完整公式求导,因为$f,i,\widetilde{C_t}$都是关于$C_{t-1}$ 的函数,因为输入有$h_{t-1}$: $$ \frac{∂C_t}{∂C_{t−1}}=\frac{\partial{C_t}}{\partial{f_t}}\frac{\partial f_t}{\partial{h_{t-1}}}\frac{\partial{h_{t-1}}}{C_{t-1}}+\frac{\partial{C_t}}{\partial{i_t}}\frac{\partial i_t}{\partial{h_{t-1}}}\frac{\partial{h_{t-1}}}{C_{t-1}}+\frac{\partial{C_t}}{\partial{\widetilde{C_t}}}\frac{\partial \widetilde{C_t}}{\partial{h_{t-1}}}\frac{\partial{h_{t-1}}}{C_{t-1}}\
\frac{∂C_t}{∂C_{t−1}}=C_{t-1}\sigma’(·)W_fo_{t-1}tanh’(C_{t-1})+\widetilde{C_{t}}\sigma’(·)W_io_{t-1}tanh’(C_{t-1})+\i_t tanh’(·)W_c*o_{t-1}tanh’(C_{t-1})+f_t $$
RNNs, the terms $\frac{\partial S_j}{\partial S_{j-1}}$will eventually take on a values that are either always above 1 or always in the range [0,1], this is essentially what leads to the vanishing/exploding gradient problem. The terms here, $\frac{∂C_t}{∂C_{t−1}}$, at any time step can take on either values that are greater than 1 or values in the range [0,1]. Thus if we extend to an infinite amount of time steps, it is not guarenteed that we will end up converging to 0 or infinity (unlike in vanilla RNNs). If we start to converge to zero, we can always set the values of $f_t$ (and other gate values) to be higher in order to bring the value of $\frac{∂C_t}{∂C_{t−1}}$closer to 1, thus preventing the gradients from vanishing (or at the very least, preventing them from vanishing too quickly). One important thing to note is that the values $f_t,o_t,i_t$, and $\widetilde{C_{t}}$are things that the network learns to set (conditioned on the current input and hidden state). Thus, in this way the network learns to decide when to let the gradient vanish, and whento preserve it, by setting the gate values accordingly!
This might all seem magical, but it really is just the result of two main things:
- The additive update function for the cell state gives a derivative thats much more ‘well behaved’
- The gating functions allow the network to decide how much the gradient vanishes, and can take on different values at each time step. The values that they take on are learned functions of the current input and hidden state.
补充:对于梯度爆炸问题
This does not really help with gradient explosions, if your gradients are too high there is little that the LSTM gating functions can do for you. There are two standard methods for preventing exploding gradients: 1)Hope and pray that you don’t get them while training, 2)or use gradient clipping.The latter has a greater success rate, however I have had some success with the former,
参考链接
https://weberna.github.io/blog/2017/11/15/LSTM-Vanishing-Gradients.html(很好)
https://zhuanlan.zhihu.com/p/28687529
https://zhuanlan.zhihu.com/p/28749444
https://www.zhihu.com/question/44895610/answer/154565425
https://blog.csdn.net/hx14301009/article/details/80401227