理解
堆分为最大堆和最小堆,这里以最大堆为例子进行讲解。

堆的概念:
堆(英语:Heap)是计算机科学中的一种特别的树状数据结构。若是满足以下特性,即可称为堆:“给定堆中任意节点 P 和 C,若 P 是 C 的母节点,那么 P 的值会小于等于(或大于等于) C 的值”。若母节点的值恒小于等于子节点的值,此堆称为最小堆(英语:min heap);反之,若母节点的值恒大于等于子节点的值,此堆称为最大堆(英语:max heap)。在堆中最顶端的那一个节点,称作根节点(英语:root node),根节点本身没有母节点(英语:parent node)。
n个元素序列${k_1, k_2… k_i…k_n}$,当且仅当满足下列关系时称之为堆: $(k_i <= k_{2i}, k_i <= k_{2i+1)}$或者$(k_i >= k_{2i}, k_i >= k_{2i+1}), (i = 1, 2, 3, 4… n/2)$
在队列中,调度程序反复提取队列中第一个作业并运行,因为实际情况中某些时间较短的任务将等待很长时间才能结束,或者某些不短小,但具有重要性的作业,同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。[1] ~维基百科
堆排序
基本操作
| 操作 | 描述 | 时间复杂度 |
|---|---|---|
| build | 创建一个空堆 | $O(n)$ |
| insert | 向堆中插入一个新元素 | $O(log n)$ |
| get | 获取当前堆顶元素的值 | $O(1)$ |
| delete | 删除堆顶元素 | $O(\log n) $ |
性质

堆一般用数组或者vector来存储,通过索引的操作虚拟一个完全二叉树结构。其性质有:
- 任意节点小于(或大于)它的所有后裔,最小元(或最大元)在堆的根上(堆序性)。
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
常见的堆有二叉堆、斐波那契堆等。
原理
虽然理论容易理解,但是要真正把这个算法搞通,包括能直接手写算法,在实现的时候还是会觉得有一点难度。这里需要谨记的是 给定一个根节点, 若其左子树和右子树同时满足堆的条件后,对根节点完成下沉操作后,整个树🌲一定是一个堆。
完全二叉树的节点索引关系 假设有一个数组从1开始的size为n的数组arr。其最后一个非叶子节点的索引为$start=(n/2)$,该非叶子节点的左儿子为$start2$,右儿子为$start2+1$;注意,若数组从0开始,其最后一个非叶子节点的索引为$start=(n/2-1)$,该非叶子节点的左儿子为$start2+1$,右儿子为$start2+2$,以下部分,包括实现,都是从0开始的。
基本操作
这里只解说,几个比较难的操作。
第一步:build-构建最大堆
给定一个输入数组,可以得到如下的一个初始完全二叉树
 为了得到一个堆,build操作需要从这个二叉树的最后一个非叶子节点开始,对所有的非叶子节点进行下沉操作,也就是MaxHeap构造函数中下面的代码:
为了得到一个堆,build操作需要从这个二叉树的最后一个非叶子节点开始,对所有的非叶子节点进行下沉操作,也就是MaxHeap构造函数中下面的代码:
int curPos=size/2-1;//最后一个非叶子节点
while(curPos>=0)//循环下沉所有叶子节点
{
shift_down(curPos,arrSize-1);//下沉操作
curPos--;//非叶子节点的位置
}
最终得到这样一个堆:
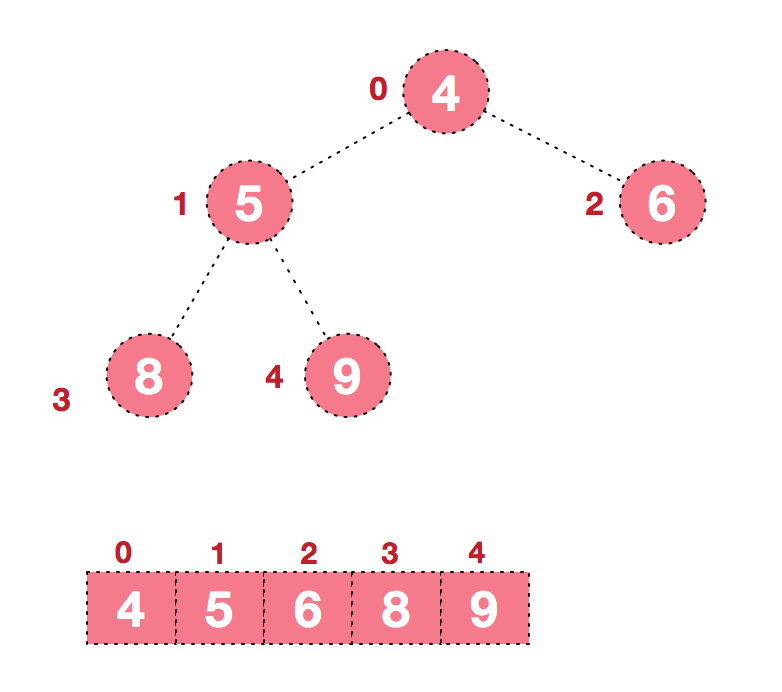
下沉 这个地方需要讲解一下下沉操作。下沉每个节点的时候,都要保证其做子树和右子树都是一个堆,这也是为什么构建堆时,下沉操作是从最后一个非叶子节点开始的。我们再回忆前面的关键概念:给定一个树的根节点, 若其左子树和右子树同时满足堆的条件后,对根节点完成下沉操作后,整个树🌲一定是一个堆。
下沉操作是通过一个循环来实现的,循环是为了保证下沉能够完全进行,也就是说有可能下沉一次,交换了两个节点的值,会导致子树不再满足堆的性质,这个时候,这个节点还需要继续下沉。也就是下面的例子:4要下沉两次。
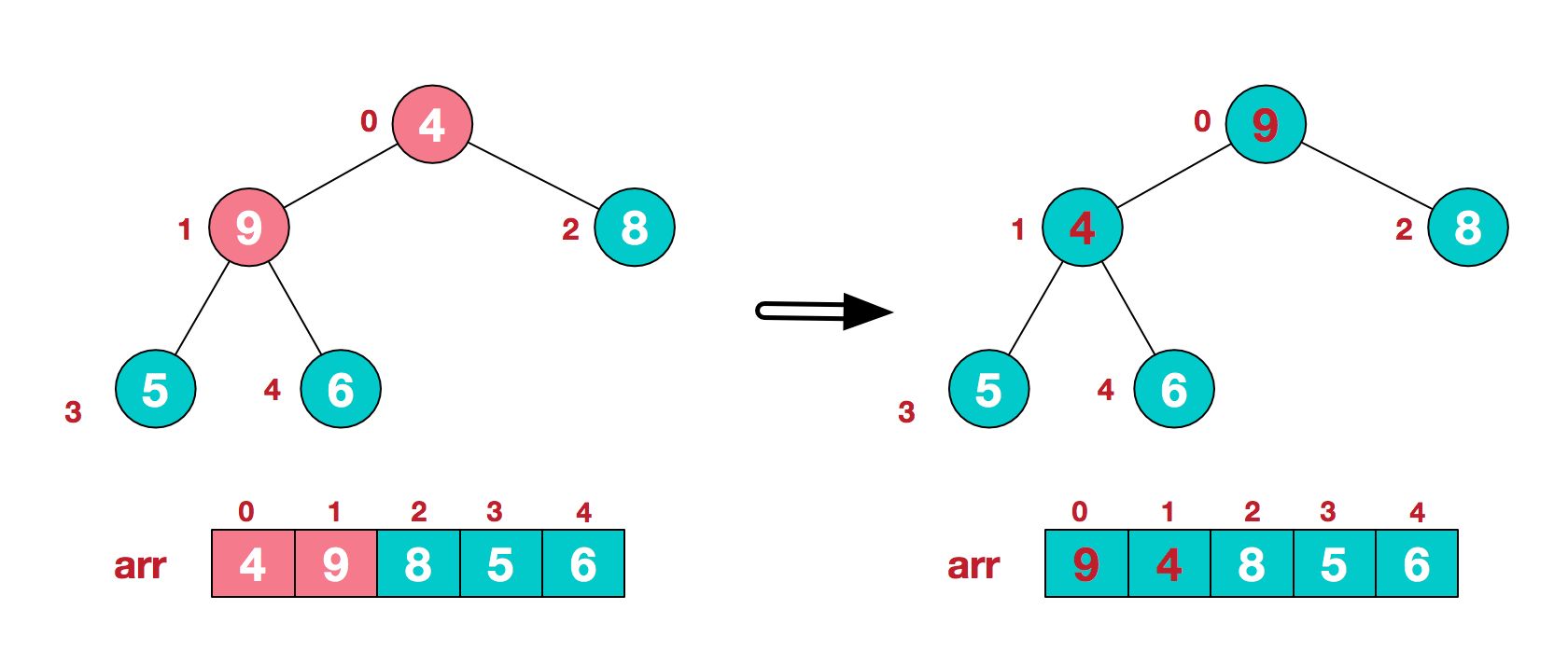

T temp=heap[i];//当前非叶子节点
while (j<=end)//是否继续进行往下沉的条件
{
if(j+1<end&&heap[j]>heap[j+1])//找到两个儿子节点更大的一个
{
j++;
}
if(temp<heap[j])break;//表示此节点i已经满足堆的条件,不需要继续往下沉;
//否则,会继续往下判断
heap[i]=heap[j];
i=j;//新的节点
j=2*j+1;//新节点的左子节点
}
heap[i]=temp;//完成两个节点的交换,也可能是heap[i]和自身的赋值,比如在while循环的第一遍循环就break出去。
这个地方还需要注意的是对新的非叶子节点索引的计算以及左儿子索引非计算。
堆的插入和删除操作
堆构建完成后,我们可以进行插入和删除操作,插入操作的思想就是讲元素插入到堆的末尾,也就是数组的末尾,堆的尺寸加1,然后对这个末尾的新元素进行上浮操作,也就是说一直向上移动该元素,直到其父节点大于该元素。若插入前,该数组的大小为size,那么新元素的父节点索引就是$i=(size-1)/2$,若一次上浮无法满足堆的性质,就计算新的父节点i=$(i-1)/2$。
T temp=heap[j];
while (j>=0)
{
if(temp<heap[i])//插入的时候就已经满足堆的条件,则不需要再继续上浮了
{
break;
} else {//插入时不满足,上浮
heap[j]=heap[i];
}
j=i;//j指向其父节点
i=(i-1)/2;//j为新j的父节点
}
heap[j]=temp;//完成交换
对于删除操作呢,就比较简单了,就是交换堆顶元素和最后一个元素的值,堆的尺寸减1,然后对根节点进行下沉操作即可,因为我们要时刻记得:给定一个树的根节点, 若其左子树和右子树同时满足堆的条件后,对根节点完成下沉操作后,整个树🌲一定是一个堆。所以删除操作就没有什么复杂的操作了。
堆排序实现
要注意空堆和堆容量的判断,还有堆的尺寸要注意改变。
基类
#ifndef SORT_HEAP_H
#define SORT_HEAP_H
enum{DEFAUKT_SIZE=10};
template <typename T>
class Heap
{
public:
Heap()=default;
virtual ~Heap()= default;
virtual void show_heap()const =0;
virtual bool insert_heap(const T&)=0;
virtual bool remove_heap(T&)=0;
};
#endif //SORT_HEAP_H
最大堆
头文件
#ifndef SORT_MAXHEAP_H
#define SORT_MAXHEAP_H
#include "heap.h"
template <typename T>
class MaxHeap: public Heap<T> {
public:
/**
* 创建一个空堆
*/
MaxHeap(int sz=DEFAUKT_SIZE);
/**
* 根据已有数组堆创建一个堆
*/
MaxHeap(const T[],const int );
/**
* 析构函数
*/
~MaxHeap();
/**
* 显示堆
*/
void show_heap()const;
/**
* 向堆中插入元素
* @return
*/
bool insert_heap(const T&);
/**
* 移除堆中的元素
* @return
*/
bool remove_heap(T&);
protected:
/**
* 下浮
*/
void shift_down(int,int);
/**
* 上浮
*/
void shift_up(int);
private:
//指向堆的指针
T *heap;
//已有堆中元素个数
int size;
//堆的容量
int capacity;
};
#endif //SORT_MAXHEAP_H
cpp文件
#include <form.h>
#include "MaxHeap.h"
template <typename T>
MaxHeap<T>::MaxHeap(int sz) {
capacity=sz>DEFAUKT_SIZE?sz:DEFAUKT_SIZE;
heap=new T[capacity];
assert(heap!= nullptr);
size=0;
}
template <typename T>
MaxHeap<T>::MaxHeap(const T arr[],const int arrSize)
{
capacity=arrSize>DEFAUKT_SIZE?arrSize:DEFAUKT_SIZE;
heap=new T[capacity];
size=arrSize;
for(int i=0;i<arrSize;i++)
{
heap[i]=arr[i];
}
int curPos=size/2-1;
while(curPos>=0)
{
shift_down(curPos,arrSize-1);
curPos--;
}
}
template <typename T>
void MaxHeap<T>::shift_down(int start, int end) {
int i=start;//第i个非叶子节点
int j=start*2+1;//第i个非叶子节点的左儿子
T temp=heap[i];
while (j<=end)//是否继续进行往下沉的条件
{
if(j+1<end&&heap[j]>heap[j+1])//找到两个儿子节点更大的一个
{
j++;
}
if(temp<heap[j])break;//表示此节点i已经满足堆的条件,不需要继续往下沉;
//否则,会继续往下判断
heap[i]=heap[j];
i=j;//新的节点
j=2*j+1;//新节点的左子节点
}
heap[i]=temp;//完成两个节点的交换,也可能是heap[i]和自身的赋值,比如在while循环的第一遍循环就break出去。
}
template <typename T>
MaxHeap<T>::~MaxHeap() {
delete heap;
heap= nullptr;
capacity=size=0;
}
template <typename T>
void MaxHeap<T>::shift_up(int e) {
int j=e;//j为最后新加入的元素
int i=(e-1)/2;//j的父节点
T temp=heap[j];
while (j>=0)
{
if(temp<heap[i])//插入的时候就已经满足堆的条件
{
break;
} else {//插入时不满足
heap[j]=heap[i];
}
j=i;//j指向其父节点
i=(i-1)/2;//j为新j的父节点
}
heap[j]=temp;//完成交换
}
template<typename T>
bool MaxHeap<T>::insert_heap(const T &val) {
if(size>=capacity)return false;
heap[size]=val;
shift_up(size);
size+=1;
return true;
}
template <typename T>
bool MaxHeap<T>::remove_heap(T &val) {
if(size<=0)return false;
val=heap[0];
heap[0]=heap[size-1];
--size;
shift_down(0,size-1);//这里root就是数组的第一个元素。
// 所以从0开始;而在初始建堆的时候是从最后一个非叶子节点开始下沉的,
// 这样是为了保证在下沉每个节点时,其左右子树都满足堆的条件。
}
参考资料:
代码实现:https://blog.csdn.net/FreeeLinux/article/details/52162788
理论理解:https://www.cnblogs.com/chengxiao/p/6129630.html
代码可在GitHub上获取:https://github.com/Narcissuscyn/Algorithm