RNN原理、公式推导及python实现

RNN原理及pytorch实现

RNN原理及pytorch实现

图像理解

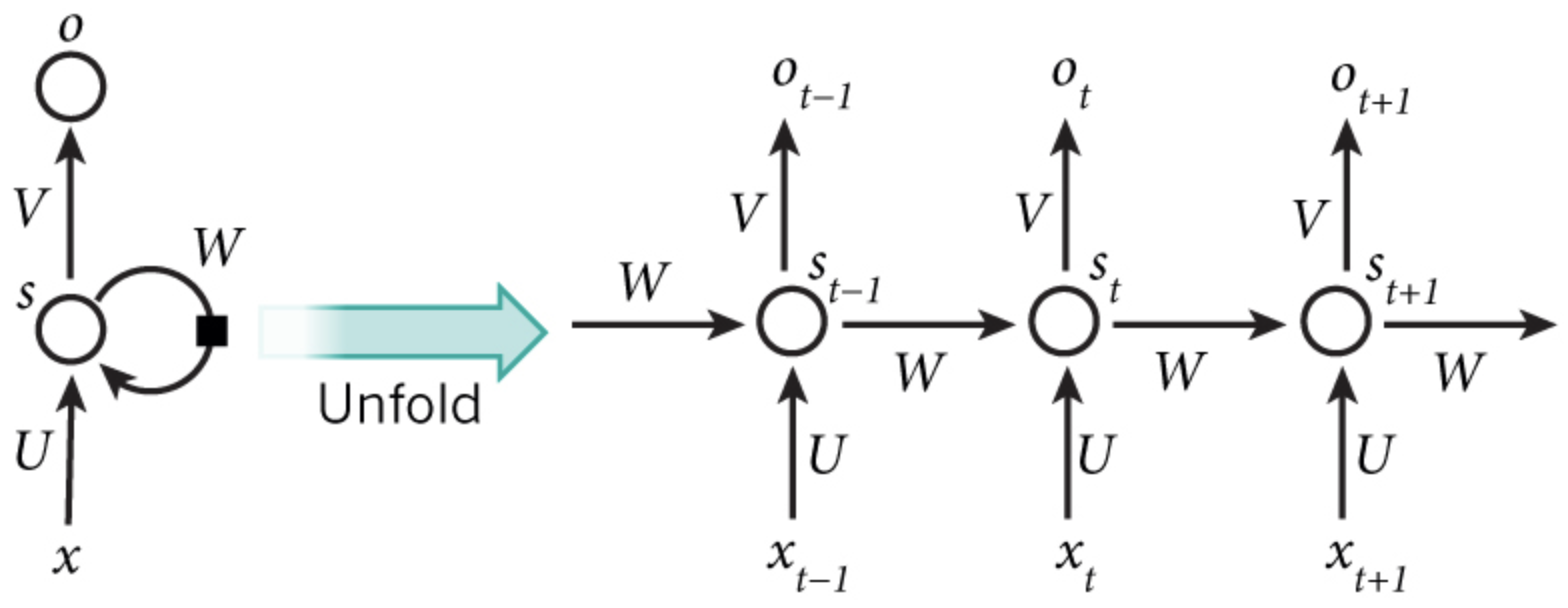
注意细节

RNN只有这四个参数：$U,W$,对于RNN和特定任务相结合，使用隐藏状态的输出，得到预测结果，也就是分类器部分，才有分类器的参数$V$，并不是RNN的参数。
横向展开的每个timestep共享权重。
pytorch中的激活函数：tanh 或者 relu,因为pytorch直接使用的cudnn接口，cudnn中只支持这两种。
pytorch中，RNN的默认输入形状是(seq_len, batch_size, input_size)，batch_size位于第二维度，因为cuDNN中RNN的API就是batch_size在第二维度！把batch_first设置为True，可以将batch_size和序列长度seq_len对换位置。batch first意味着模型的输入（一个Tensor）在内存中存储时，先存储第一个sequence，再存储第二个… 而如果是seq_len first，模型的输入在内存中，先存储所有序列的第一个单元，然后是第二个单元.

公式理解

正向传播公式

RNN迭代式 $s_t=tanh(Ux_t+Ws_{t-1})$ 分类器 $y_t=softmax(Vs_t)$ 损失:把整个timestep的数据当成一个训练数据。 $\begin{align} E_t(y_t,\hat{y_t})&=-y_tlog\hat{y_t}\\ E(y,\hat{y})&=\sum_tE_t(y_t,\hat{y_t})\\ &=-\sum_ty_tlog\hat{y_t} \end{align}$

反向求导（BPTT：back propagation through time）

BPTT是关于标准RNN的名称。对每个参数的求导，都要各个timestep加起来。即： $\frac{\partial{E}}{\partial{W}}=\sum_t\frac{\partial{E_t}}{\partial{W}}\\ \frac{\partial{E}}{\partial{U}}=\sum_t\frac{\partial{E_t}}{\partial{U}}\\ \frac{\partial{E}}{\partial{V}}=\sum_t\frac{\partial{E_t}}{\partial{V}}$

以$\frac{\partial{E_1}}{\partial{W}}$为例：

1）$V$的反向求导比较简单， $\frac{\partial{E_t}}{\partial{V}}$ ,与等无时间序列无关 $\begin{align} E_t&=-y_t^Tlog(\hat{y_t})\\ z_t&=Vs_t\\ \hat{y_t}&=softmax(z_t) \end{align}$

根据链式法则： $$ \begin{align} \frac{\partial{E_t}}{\partial{V}}&=\frac{\partial{E_t}}{\partial{\hat{y_t}}}·\frac{\partial{\hat{y_t}}}{\partial{z_t}}·\frac{\partial{z_t}}{\partial{V}}
&=(-y_t^T·\frac{1}{\hat{y_t}})(\frac{\partial{\hat{y_t}}}{\partial{z_t}})(s_t)
&=(\hat{y_t}-y_t^T)\otimes s_t

\end{align} $$ 注意：这里$z_t,y_t$都是向量,$\frac{\partial{\hat{y_t}}}{\partial{z_t}}$这个导数就是softmax的求导，因此是个分段函数，根据下面补充的结论，可推出最后的结果。最后的外积，是根据纬度推导出来的，比如有k个类，$\hat{y_t},y_t$都是k维的，$s_t$为隐藏状态输出，是h维的，而V是个矩阵，也就是$k\times h$维的（左乘），因此，就是外积。

补充：

注softmax求导

$\begin{equation} g(x_i)=\frac{e^{x_i}}{\sum_j{e^{x_j}}}\\ \frac{\partial{g(x_i)}}{\partial{x_j}}=\left\{ \begin{aligned} g(x_i)(1-g(x_i)),i=j \\ g(x_i)g(x_j),i\neq j \end{aligned} \right. \end{equation}$

推导过程：

cross entropy loss 求导 $E_t=y_t^Tlog(\hat{y_t})\\ \frac{\partial{E}}{\partial{\hat{y_t}}}=(-y_t^T·\frac{1}{\hat{y_t}})$
总结：softmax+cross entropy loss ,对$x_j$（这里可以看成是$z_{tj}$）求导，就是t==j时，对应位置的softmax值（也就是预测分数）减1，其他的不变： $$ \hat{y_t}=g(x_t)\

\frac{\partial{E_t}}{\partial{x_j}}=\left{ \begin{aligned} \hat{y_t}-1,t=j
\hat{y_j},t\neq j \end{aligned} \right. $这里$y_t$对应了标签t,如果把标签表示成one-hot的，那么就是：$ \frac{\partial{E_t}}{\partial{x}}=\frac{\partial{E_t}}{\partial{z_t}}=(\hat{y_t}-y_t^T) $$

2）$W$的反向求导：

首先要得到$E_t$对$s_t$的导数（$(\hat{y_t}-y_t^T)$是k维（分类类别数），V是k*h的）：

$\begin{aligned} \frac{\partial{E_t}}{s_t}&=\frac{\partial{E_t}}{\partial{z_t}}\\ &=V^T(\hat{y_t}-y_t^T) \end{aligned}$

$s_t$对W求导 $$ s_t=tanh(Ws_{t-1}+Ux_t)\

\frac{\partial s_t}{\partial W}=(1-s_t^2)s_{t-1}\

\frac{\partial E_t}{\partial W}=V^T(\hat{y_t}-y_t^T)(1-s_t^2)s_{t-1} $$ 注：需要注意的是各部分之间的运算时element-wise dot ,outer times还是dot,这个需要根据纬度再来推导。
- 补充： $f(t)=tanh(t)\\ \frac{\partial{f}}{\partial{t}}=1-f(t)^2$

3）$U$的反向求导:$\frac{\partial{E_t}}{\partial{U}}$,和W推导过程的一样： $\frac{\partial{E_t}}{\partial{U}}=V^T(\hat{y_t}-y_t^T)(1-s_t^2)x_t$

实现

def bptt(self, x, y):

    T = len(y)

    # Perform forward propagation

    o, s = self.forward_propagation(x)

    # We accumulate the gradients in these variables

    dLdU = np.zeros(self.U.shape)

    dLdV = np.zeros(self.V.shape)

    dLdW = np.zeros(self.W.shape)

    delta_o = o

    delta_o[np.arange(len(y)), y] -= 1.

    # For each output backwards...

    for t in np.arange(T)[::-1]:

        dLdV += np.outer(delta_o[t], s[t].T)

        # Initial delta calculation: dL/dz

        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))

        # Backpropagation through time (for at most self.bptt_truncate steps)

        for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:

            # print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)

            # Add to gradients at each previous step

            dLdW += np.outer(delta_t, s[bptt_step-1])              

            dLdU[:,x[bptt_step]] += delta_t#这个地方不容易想到，本来应该是delta_t与x_t的外积（delta_t是h维的，x_t是d维的，U是h*d的，因为U对x_t是左乘），但是这里省略了这个乘法.因为X是输入句子中，单词在字典中是否出现，那么，就是one-hot的表示，因此可以省略这个外积运算，直接对标签为1的+delta_t即可。

            # Update delta for next step dL/dz at t-1

            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)/#求s_t对s_{t-1}的导数，下一次循环就是s_{t-1}对U,W的导数了.

    return [dLdU, dLdV, dLdW]

参考资料

https://zhuanlan.zhihu.com/p/32103001

https://zhuanlan.zhihu.com/p/32930648

https://github.com/pangolulu/rnn-from-scratch

https://www.cnblogs.com/wacc/p/5341670.html